Le meilleur des deux mondes – l’assurance mixte
Cynthia connaît bien la famille de Miss Cathleen et leur situation financière. Elle lui propose d’anticiper les frais de maison de retraite et d’ajouter à son contrat une composante d’épargne qui verse 80 000 EUR si elle est en vie à 75 ans. Miss Cathleen souhaite financer cette assurance mixte avec des primes constantes \(P\). L’ensemble du montage est illustré sur la frise chronologique suivante.
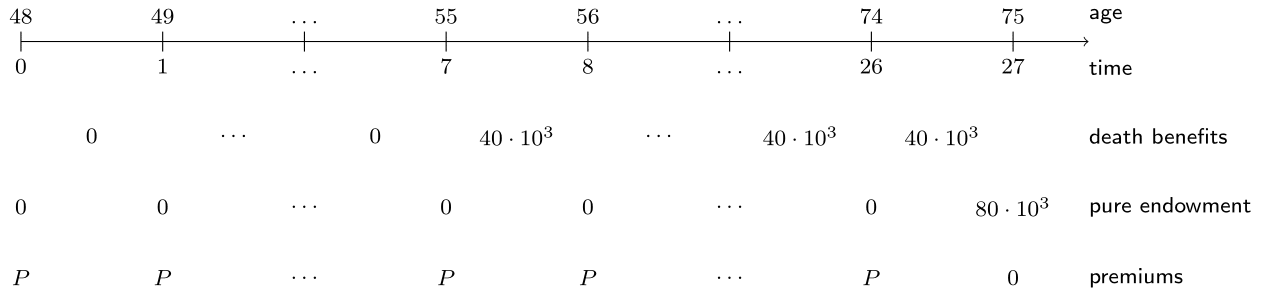
Les probabilités de survie px, le taux d’intérêt i et EPV_death_benefits, que vous avez calculés dans l’exercice précédent, sont disponibles dans votre espace de travail. À vous maintenant de déterminer le niveau de prime \(P\).
Cet exercice fait partie du cours
Évaluation des produits d’assurance vie en R
Instructions
- Déterminez la VAP de la dotation pure en multipliant la prestation de 80 000, le facteur d’actualisation \((1 + i) ^ {-27}\) et la probabilité de survie \(_{27}p_{48}\).
- Calculez la VAP du schéma de primes et affectez le résultat à
EPV_rho. - Affichez le niveau de prime \(P\) en utilisant le principe d’équivalence actuarielle.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Pure endowment
EPV_pure_endowment <- ___ * (1 + i) ^ - 27 * prod(px[(___):(___)])
EPV_pure_endowment
# Premium pattern
kpx <- c(___, cumprod(px[(___):(___)]))
discount_factors <- (___) ^ - (0:(length(kpx) - 1))
rho <- rep(1, length(kpx))
EPV_rho <- ___
EPV_rho
# Premium level
(___ + ___) / ___