Partout, à tout moment ?
En réfléchissant à ses habitudes de dépense, Cynthia se demande combien d’argent elle obtiendrait si, au lieu d’acheter des téléchargements et des billets de concert, elle plaçait son argent sur un compte bancaire. Pour cela, vous allez calculer la valeur des flux de trésorerie à une date future, en utilisant une fonction d’actualisation appropriée.
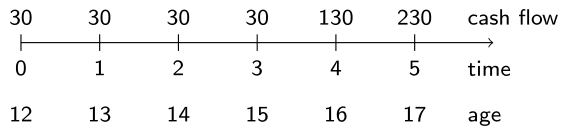
Le profil de dépenses de Cynthia est illustré ci-dessus. Le vecteur cash_flows, que vous avez défini dans le premier exercice, a été préchargé dans votre espace de travail. Le taux d’intérêt est toujours de 2 %.
Cet exercice fait partie du cours
Évaluation des produits d’assurance vie en R
Instructions
- Définissez la fonction
discount()qui calcule la valeur à l’instant \(s\) de 1 EUR versé à l’instant \(t\). - Utilisez
discount()pour calculer la valeur actuelle decash_flowsaux dates 0 à 5. Vous devriez retrouver votre résultat précédent, à savoir 444,93 EUR. - Affichez la valeur du vecteur de flux de trésorerie lorsque Cynthia aura 18 ans, dans 6 ans.
- Calculez la valeur accumulée du vecteur de flux à l’instant 6 d’une autre manière : cette fois, convertissez la
present_valueà l’instant 0 en valeur à l’instant 6.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Define the discount function v
discount <- function(s, t, i = 0.02) {
(1 + ___) ^ - (___ - ___)
}
# Calculate the present value
present_value <- sum(cash_flows * discount(___, ___))
present_value
# Calculate the value at time 6
sum(cash_flows * discount(___, ___))
# Calculate the value at time 6, starting from present_value
present_value * discount(___, ___)