Inferenz für den posterioren Trend
Erinnere dich an die Likelihood des Bayes’schen Regressionsmodells des Gewichts \(Y\) über die Körpergröße \(X\): \(Y \sim N(m, s^2)\), wobei \(m = a + b X\). In früheren Übungen hast du die Form des posterioren Trends \(m\) (durchgezogene Linie) angenähert. Daran siehst du, dass das typische Gewicht von 180 cm großen Erwachsenen ungefähr 80 kg beträgt (gestrichelte Linien):
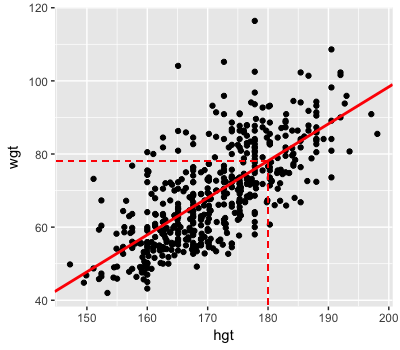
Du wirst RJAGS-Simulationsergebnisse verwenden, um den posterioren Trend beim Gewicht von 180 cm großen Erwachsenen sowie die posteriore Unsicherheit in diesem Trend zu approximieren. Die RJAGS-Simulation des Posteriors mit 100.000 Iterationen, weight_sim_big, befindet sich in deinem Workspace, zusammen mit einem Dataframe der Markov-Chain-Ausgaben, weight_chains.
Diese Übung ist Teil des Kurses
Bayesianisches Modellieren mit RJAGS
Anleitung zur Übung
weight_chainsenthält 100.000 Sätze posterior plausibler Parameterwerte von \(a\) und \(b\). Berechne daraus jeweils das mittlere (typische) Gewicht von 180 cm großen Erwachsenen, \(a + b * 180\). Speichere diese Trends als neue Variablem_180inweight_chains.Erstelle ein Posterior-Dichte-Diagramm der 100.000
m_180-Werte.Verwende die 100.000
m_180-Werte, um ein 95%-Credible-Interval (posteriores Glaubwürdigkeitsintervall) für das mittlere Gewicht von 180 cm großen Erwachsenen zu berechnen.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Calculate the trend under each Markov chain parameter set
weight_chains <- weight_chains %>%
mutate(m_180 = ___)
# Construct a posterior density plot of the trend
ggplot(___, aes(x = ___)) +
geom_density()
# Construct a posterior credible interval for the trend
quantile(___, probs = c(___, ___))