Monthly mortgage loan payments

Cynthia's parents receive a loan of 125,000 EUR in return for fixed monthly payments \(K\) over the next 20 years as visualized in the graph below.

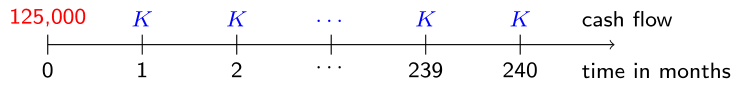
Using the variables number_payments and monthly_interest defined in the previous exercise, which are preloaded for you, it's up to you to determine the value of \(K\) based on the principle of actuarial equivalence.

Este ejercicio forma parte del curso

Life Insurance Products Valuation in R

Ver curso

Instrucciones del ejercicio

Define the discount factors corresponding to the first payment month up until the last payment month. Do this by raising 1 plus monthly_interest to the power minus a vector from 1 until number_payments.
Create the variable payments which reflects the payment pattern. This should be a vector of ones with length number_payments.
Finally, calculate the monthly payment \(K\) by dividing the mortgage amount 125,000 by the present value of the payment pattern.

Ejercicio interactivo práctico

Prueba este ejercicio y completa el código de muestra.

# Define the discount factors
discount_factors <- (___) ^ - (___)

# Define the payment pattern
payments <- rep(___, ___)

# Calculate the monthly loan payment K
K <- ___ / ___(___ * ___)
K

Editar y ejecutar código