Slope and Rates-of-Change
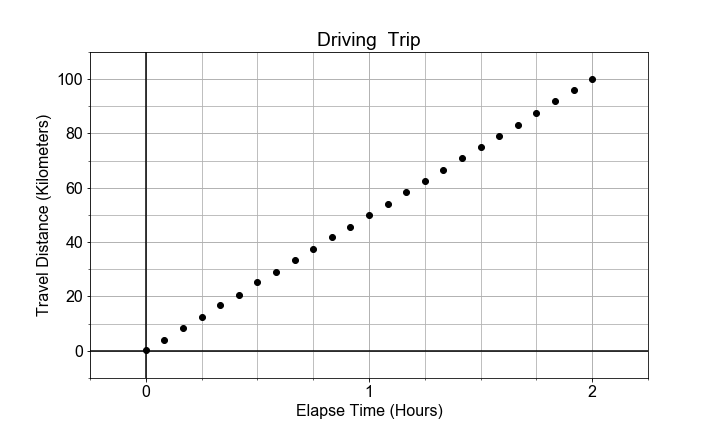
In this exercise, you will model the motion of a car driving (roughly) constant velocity by computing the average velocity over the entire trip. The linear relationship modeled is between the time elapsed and the distance traveled.
In this case, the model parameter a1, or slope, is approximated or "estimated", as the mean velocity, or put another way, the "rate-of-change" of the distance ("rise") divided by the time ("run").
This is a part of the course
“Introduction to Linear Modeling in Python”
Exercise instructions
- Compute the the point-to-point differences of both the
timesanddistancesusingnumpy.diff(). - Compute an array of
velocitiesas the ratio of thediff_distancedivided bydiff_times. - Compute the average and range of velocity values, using
numpymethodsmean,max,min. - Plot the array of
velocitiesto visualize the average and spread of the values.
Hands-on interactive exercise
Have a go at this exercise by completing this sample code.
# Compute an array of velocities as the slope between each point
diff_distances = np.diff(____)
diff_times = np.diff(____)
velocities = ____ / diff_times
# Chracterize the center and spread of the velocities
v_avg = np.____(velocities)
v_max = np.____(velocities)
v_min = np.____(velocities)
v_range = ____ - ____
# Plot the distribution of velocities
fig = plot_velocity_timeseries(times[1:], velocities)This exercise is part of the course
Introduction to Linear Modeling in Python
Explore the concepts and applications of linear models with python and build models to describe, predict, and extract insight from data patterns.
Here we look at the parts that go into building a linear model. Using the concept of a Taylor Series, we focus on the parameters slope and intercept, how they define the model, and how to interpret the them in several applied contexts. We apply a variety of python modules to find the model that best fits the data, by computing the optimal values of slope and intercept, using least-squares, numpy, statsmodels, and scikit-learn.
Exercise 1: What makes a model linearExercise 2: Terms in a ModelExercise 3: Model ComponentsExercise 4: Model ParametersExercise 5: Interpreting Slope and InterceptExercise 6: Linear ProportionalityExercise 7: Slope and Rates-of-ChangeExercise 8: Intercept and Starting PointsExercise 9: Model OptimizationExercise 10: Residual Sum of the SquaresExercise 11: Minimizing the ResidualsExercise 12: Visualizing the RSS MinimaExercise 13: Least-Squares OptimizationExercise 14: Least-Squares with `numpy`Exercise 15: Optimization with ScipyExercise 16: Least-Squares with `statsmodels`What is DataCamp?
Learn the data skills you need online at your own pace—from non-coding essentials to data science and machine learning.