Estimating Speed and Confidence

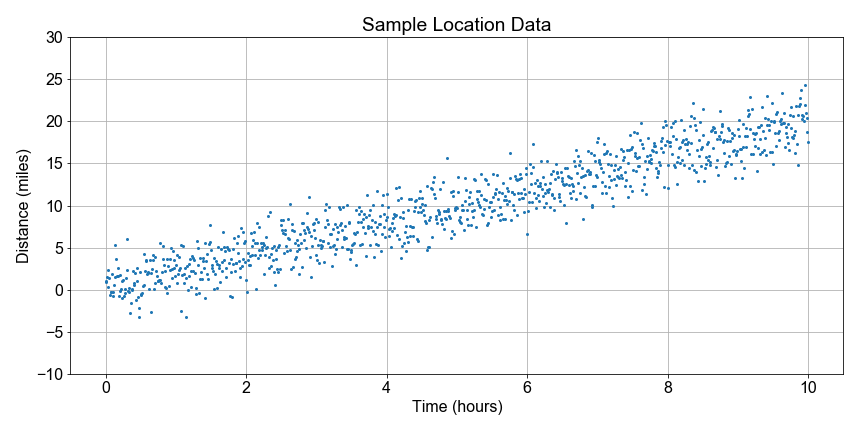
Let's continue looking at the National Park hiking data. Notice that some distances are negative because they walked in the opposite direction from the trail head; the data are messy so let's just focus on the overall trend.

In this exercise, you goal is to use boot-strap resampling to find the distribution of speed values for a linear model, and then from that distribution, compute the best estimate for the speed and the 90th percent confidence interval of that estimate. The speed here is the slope parameter from the linear regression model to fit distance as a function of time.

To get you started, we've preloaded distance and time data, together with a pre-defined least_squares() function to compute the speed value for each resample.

Use np.random.choice() to draw sample_inds from population_inds, preserving the distance-time pairing of each datum.
To preserve time ordering, .sort() the sample_inds, and then use sample_inds to index distances and times.
Use least_squares(times, distances) to compute linear model parameters and store a1 in resample_speeds.
Apply np.mean() and np.percentiles() to resample_speeds, computing speed and confidence interval ci_90, and then print both.

Exercise

Estimating Speed and Confidence

Instructions