Linear Proportionality

The definition of temperature scales is related to the linear expansion of certain liquids, such as mercury and alcohol. Originally, these scales were literally rulers for measuring length of fluid in the narrow marked or "graduated" tube as a proxy for temperature. The alcohol starts in a bulb, and then expands linearly into the tube, in response to increasing temperature of the bulb or whatever surrounds it.

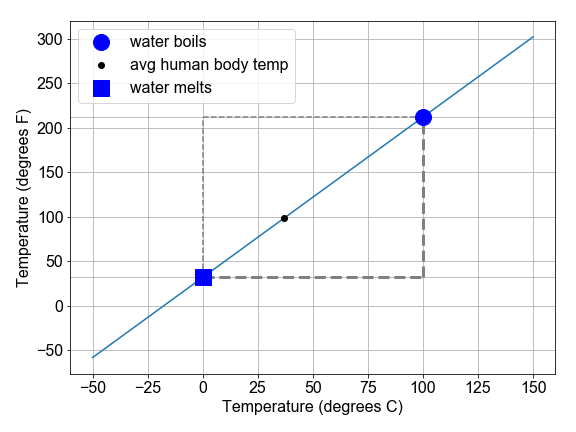
In this exercise, we will explore the conversion between the Fahrenheit and Celsius temperature scales as a demonstration of interpreting slope and intercept of a linear relationship within a physical context.

This exercise is part of the course

Introduction to Linear Modeling in Python

View Course

Exercise instructions

Complete the function temps_F = convert_scale(temps_C) as a linear model where "x" is temps_C and "y" is temps_F.
Compute the change in temperature in both scales by subtracting the freezing temperature from the boiling temperature.
Compute the slope as the change_in_F divided by the change_in_C.
Compute the intercept as the difference between the freezing points freeze_F and freeze_C.
Use the predefined plot_temperatures() to plot the resulting model.

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

# Complete the function to convert C to F
def convert_scale(temps_C):
    (freeze_C, boil_C) = (0, 100)
    (freeze_F, boil_F) = (32, 212)
    change_in_C = ____ - freeze_C
    change_in_F = ____ - freeze_F
    slope = ____ / ____
    intercept = ____ - freeze_C
    temps_F = ____ + (____ * temps_C)
    return temps_F

# Use the convert function to compute values of F and plot them
temps_C = np.linspace(0, 100, 101)
temps_F = convert_scale(temps_C)
fig = plot_temperatures(temps_C, temps_F)

Edit and Run Code