Extrapolation: Going Over the Edge

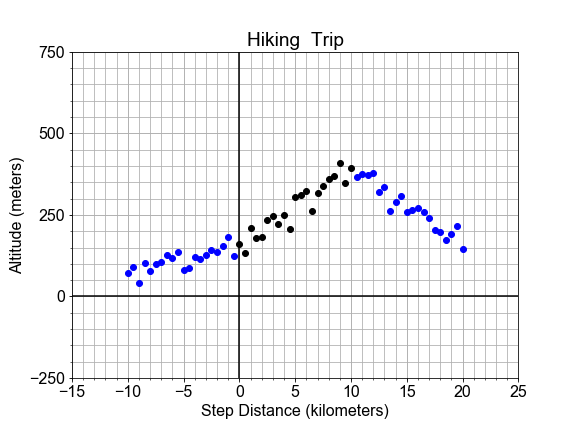
In this exercise, we consider the perils of extrapolation. Shown here is the profile of a hiking trail on a mountain. One portion of the trail, marked in black, looks linear, and was used to build a model. But we see that the best fit line, shown in red, does not fit outside the original "domain", as it extends into this new outside data, marked in blue.

If we want use the model to make predictions for the altitude, but still be accurate to within some tolerance, what are the smallest and largest values of independent variable x that we can allow ourselves to apply the model to?"

Here, use the preloaded x_data, y_data, y_model, and plot_data_model_tolerance() to complete your solution.

This exercise is part of the course

Introduction to Linear Modeling in Python

View Course

Exercise instructions

Use np.abs() to compute the residuals as the differences y_data - y_model
Find the .min() and .max() values of x at which the residuals are less than a tolerance = 100 meters.
Use np.min() andnp.max()to print the range (the largest and smallest) ofx_good` values.
Use the predefined plot_data_model_tolerance() to compare the data, model, and range of x_good values where the residuals < tolerance is True.

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

# Compute the residuals, "data - model", and determine where [residuals < tolerance]
residuals = np.abs(____ - ____)
tolerance = 100
x_good = x_data[____ < ____]

# Find the min and max of the "good" values, and plot y_data, y_model, and the tolerance range
print('Minimum good x value = {}'.format(np.____(____)))
print('Maximum good x value = {}'.format(np.____(____)))
fig = plot_data_model_tolerance(x_data, y_data, y_model, tolerance)

Edit and Run Code