Visualize the Bootstrap

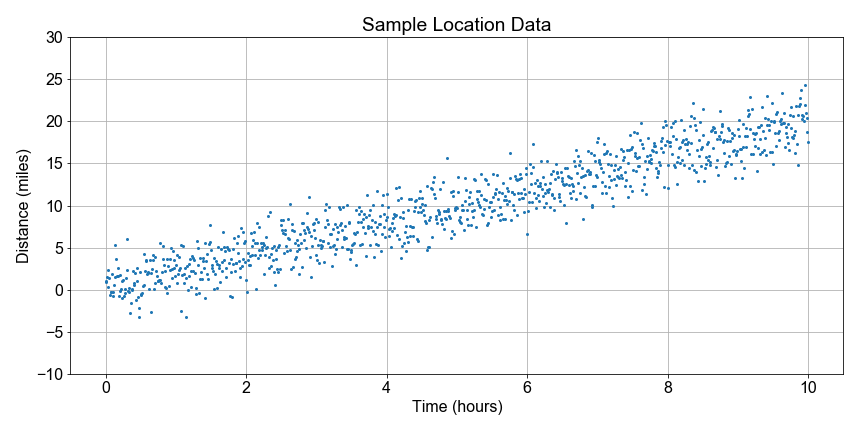
Continuing where we left off earlier in this lesson, let's visualize the bootstrap distribution of speeds estimated using bootstrap resampling, where we computed a least-squares fit to the slope for every sample to test the variation or uncertainty in our slope estimation.

To get you started, we've preloaded a function compute_resample_speeds(distances, times) to do the computation of generate the speed sample distribution.

This exercise is part of the course

Introduction to Linear Modeling in Python

View Course

Exercise instructions

Use the pre-defined compute_resample_speeds(distances, times) to compute the resample_speeds.
Use np.mean() to compute the speed_estimate from the resample_speeds.
Use np.percentile() with [5, 95] to compute the percentiles of resample_speeds, which define the confidence interval boundaries.
Use axis.hist() to plot the resample_speeds, specifying the bins with hist_bin_edges.
Using axis.axvline, specify the correct two indices of percentiles to mark the confidence interval boundaries on the chart.

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

# Create the bootstrap distribution of speeds
resample_speeds = compute_resample_speeds(____, ____)
speed_estimate = np.mean(____)
percentiles = np.percentile(____, [5, 95])

# Plot the histogram with the estimate and confidence interval
fig, axis = plt.subplots()
hist_bin_edges = np.linspace(0.0, 4.0, 21)
axis.hist(____, ____, color='green', alpha=0.35, rwidth=0.8)
axis.axvline(speed_estimate, label='Estimate', color='black')
axis.axvline(percentiles[____], label=' 5th', color='blue')
axis.axvline(percentiles[____], label='95th', color='blue')
axis.legend()
plt.show()

Edit and Run Code