Residual Sum of the Squares

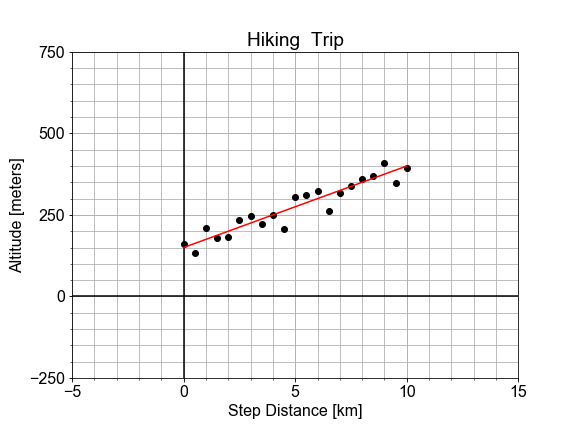
In a previous exercise, we saw that the altitude along a hiking trail was roughly fit by a linear model, and we introduced the concept of differences between the model and the data as a measure of model goodness.

In this exercise, you'll work with the same measured data, and quantifying how well a model fits it by computing the sum of the square of the "differences", also called "residuals".

This exercise is part of the course

Introduction to Linear Modeling in Python

View Course

Exercise instructions

Load the x_data, y_data with the pre-defined load_data() function.
Call the pre-defined model(), passing in x_dataand specific values a0, a1.
Compute the residuals as y_data - y_model and then find rss by using np.square() and np.sum().
Print the resulting value of rss.

Hands-on interactive exercise

Have a go at this exercise by completing this sample code.

# Load the data
x_data, y_data = load_data()

# Model the data with specified values for parameters a0, a1
y_model = model(____, a0=150, a1=25)

# Compute the RSS value for this parameterization of the model
rss = np.sum(np.square(____ - ____))
print("RSS = {}".format(____))

Edit and Run Code