LoslegenKostenlos loslegen

Extrapolation: über den Rand hinausgehen

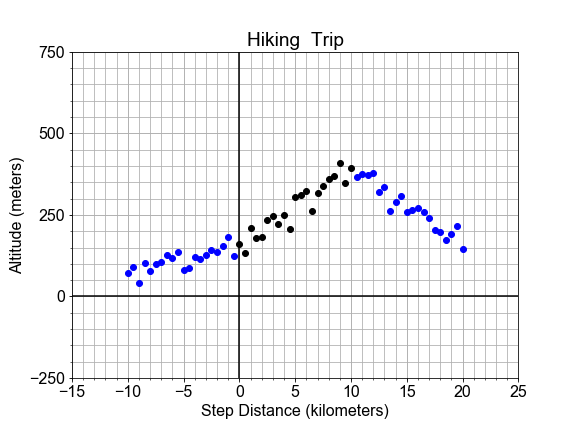
In dieser Übung schauen wir uns die Risiken der Extrapolation an. Hier siehst du das Profil eines Wanderwegs auf einem Berg. Ein Abschnitt des Wegs, schwarz markiert, wirkt linear und wurde verwendet, um ein Modell zu erstellen. Wir sehen aber, dass die Ausgleichsgerade, rot dargestellt, außerhalb des ursprünglichen „Definitionsbereichs“ nicht passt, da sie in neue, außerhalb liegende Daten (blau markiert) hineinragt.

Wenn wir das Modell verwenden möchten, um die Höhe vorherzusagen, dabei aber innerhalb einer bestimmten Toleranz genau bleiben wollen: Was sind die kleinsten und größten Werte der unabhängigen Variablen x, für die wir das Modell anwenden können?

Verwende hierzu die vorab geladenen Variablen x_data, y_data, y_model sowie plot_data_model_tolerance(), um deine Lösung zu vervollständigen.

Diese Übung ist Teil des Kurses

Einführung in lineares Modellieren mit Python

Kurs anzeigen

Anleitung zur Übung

  • Verwende np.abs(), um die Residuen als Differenzen y_data - y_model zu berechnen.
  • Ermittle die .min()- und .max()-Werte von x, bei denen die residuals kleiner sind als eine tolerance = 100 Meter.
  • Verwende np.min() und np.max(), um den Bereich (die größten und kleinsten) der x_good-Werte auszugeben.
  • Nutze die vordefinierte Funktion plot_data_model_tolerance(), um Daten, Modell und den Bereich der x_good-Werte zu vergleichen, bei denen residuals < tolerance True ist.

Interaktive Übung

Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.

# Compute the residuals, "data - model", and determine where [residuals < tolerance]
residuals = np.abs(____ - ____)
tolerance = 100
x_good = x_data[____ < ____]

# Find the min and max of the "good" values, and plot y_data, y_model, and the tolerance range
print('Minimum good x value = {}'.format(np.____(____)))
print('Maximum good x value = {}'.format(np.____(____)))
fig = plot_data_model_tolerance(x_data, y_data, y_model, tolerance)
Code bearbeiten und ausführen