LoslegenKostenlos starten

Lineare Proportionalität

Die Definition von Temperaturskalen hängt mit der linearen Ausdehnung bestimmter Flüssigkeiten zusammen, etwa Quecksilber und Alkohol. Ursprünglich waren diese Skalen wortwörtlich Lineale, die die Länge der Flüssigkeit in einem schmalen, markierten oder „graduierten“ Rohr als Stellvertreter für die Temperatur gemessen haben. Der Alkohol startet in einer Kugel und dehnt sich mit steigender Temperatur der Kugel oder der Umgebung linear in das Rohr aus.

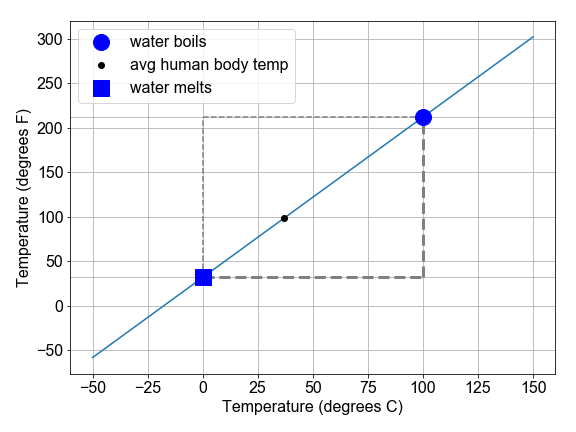
In dieser Übung untersuchen wir die Umrechnung zwischen den Fahrenheit- und Celsius-Skalen, um zu zeigen, wie man Steigung und Achsenabschnitt einer linearen Beziehung im physikalischen Kontext interpretiert.

Diese Übung ist Teil des Kurses

<Kurs>Einführung in lineares Modellieren mit Python</Kurs>
Kurs ansehen

Übungsanweisungen

  • Vervollständige die Funktion temps_F = convert_scale(temps_C) als lineares Modell, wobei „x“ temps_C und „y“ temps_F ist.
  • Berechne die Temperaturänderung in beiden Skalen, indem du die Gefriertemperatur von der Siedetemperatur subtrahst.
  • Berechne die slope als change_in_F geteilt durch change_in_C.
  • Berechne den intercept als die Differenz zwischen den Gefrierpunkten freeze_F und freeze_C.
  • Verwende die vorgegebene Funktion plot_temperatures(), um das resultierende Modell zu zeichnen.

Interaktive praktische Übung

Versuche dich an dieser Übung, indem du diesen Beispielcode vervollständigst.

# Complete the function to convert C to F
def convert_scale(temps_C):
    (freeze_C, boil_C) = (0, 100)
    (freeze_F, boil_F) = (32, 212)
    change_in_C = ____ - freeze_C
    change_in_F = ____ - freeze_F
    slope = ____ / ____
    intercept = ____ - freeze_C
    temps_F = ____ + (____ * temps_C)
    return temps_F

# Use the convert function to compute values of F and plot them
temps_C = np.linspace(0, 100, 101)
temps_F = convert_scale(temps_C)
fig = plot_temperatures(temps_C, temps_F)
Code bearbeiten und ausführen