Kovarianz vs. Korrelation

Die Kovarianz misst, ob zwei Variablen gemeinsam schwanken ("variieren"). Sie wird berechnet, indem man punktweise die Produkte der Abweichungen aus der vorherigen Übung bildet, dx[n]*dy[n], und anschließend den Mittelwert all dieser Produkte bestimmt.

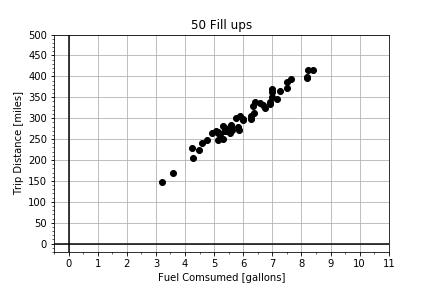
Die Korrelation ist im Kern die normalisierte Kovarianz. In dieser Übung bekommst du zwei Datenarrays, die stark korreliert sind. Du wirst sowohl die covariance als auch die correlation visualisieren und berechnen.

Diese Übung ist Teil des Kurses

<Kurs>Einführung in lineares Modellieren mit Python</Kurs>

Kurs ansehen

Übungsanweisungen

Berechne die Abweichungen dx und dy, indem du den Mittelwert mit np.mean() abziehst, und berechne die covariance als Mittelwert ihres Produkts dx*dy.
Berechne die normalisierten Abweichungen zx und zy, indem du durch die Standardabweichung mit np.std() teilst, und berechne die correlation als Mittelwert ihres Produkts zx*zy.
Verwende plot_normalized_deviations(zx, zy), um das Produkt der normalisierten Abweichungen zu plotten und es visuell mit dem Korrelationswert abzugleichen.

Interaktive praktische Übung

Versuche dich an dieser Übung, indem du diesen Beispielcode vervollständigst.

# Compute the covariance from the deviations.
dx = x - np.____(x)
dy = y - np.____(y)
covariance = np.____(____ * ____)
print("Covariance: ", covariance)

# Compute the correlation from the normalized deviations.
zx = dx / np.____(x)
zy = dy / np.____(y)
correlation = np.____(____ * ____)
print("Correlation: ", correlation)

# Plot the normalized deviations for visual inspection. 
fig = plot_normalized_deviations(zx, zy)

Code bearbeiten und ausführen