Variation in zwei Teilen
Gegeben sind zwei Datensätze mit Distanz-gegen-Zeit-Daten: einer mit sehr kleiner Geschwindigkeit und einer mit großer Geschwindigkeit. Beachte, dass beide denselben Standardfehler der Steigung haben können, aber je nach Größe der Steigung ("Effektgröße") im Vergleich zum Standardfehler ("Unsicherheit") ein unterschiedliches R-Quadrat für das Gesamtmodell.
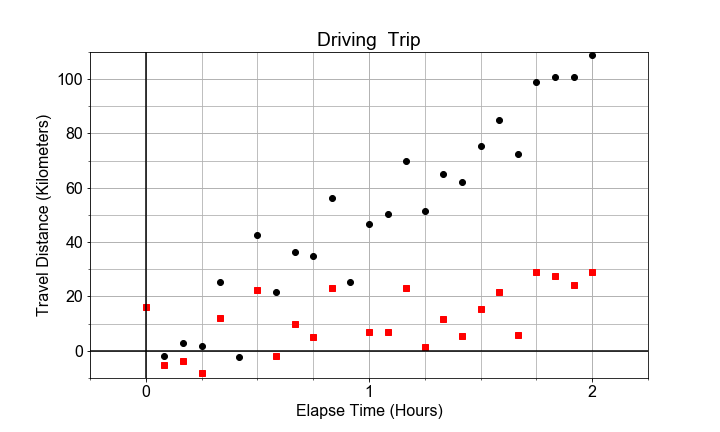
Wenn wir beide Datensätze als Streudiagramme in denselben Achsen darstellen, wird der Kontrast deutlich. Variation durch die Steigung unterscheidet sich von der Variation durch das zufällige Streuen um die Trendlinie. In dieser Übung sollst du den Standardfehler und das R-Quadrat für zwei Datensätze berechnen und vergleichen.
Diese Übung ist Teil des Kurses
Einführung in lineares Modellieren mit Python
Anleitung zur Übung
- Baue und
fit()einols()-Modell für beide Datensätzedistances1unddistances2. - Verwende die
.bseder resultierenden Modellemodel_1undmodel_2sowie den Schlüssel'times', um die Standardfehler der Steigung aus jedem Modell zu extrahieren. - Verwende das Attribut
.rsquared, um den R-Quadrat-Wert aus jedem Modell zu extrahieren. - Gib die resultierenden
se_1,rsquared_1,se_2,rsquared_2aus und vergleiche sie visuell.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Build and fit two models, for columns distances1 and distances2 in df
model_1 = ols(formula="____ ~ times", data=df).____()
model_2 = ols(formula="____ ~ times", data=df).____()
# Extract R-squared for each model, and the standard error for each slope
se_1 = model_1.____['times']
se_2 = model_2.____['times']
rsquared_1 = model_1.____
rsquared_2 = model_2.____
# Print the results
print('Model 1: SE = {:0.3f}, R-squared = {:0.3f}'.format(____, ____))
print('Model 2: SE = {:0.3f}, R-squared = {:0.3f}'.format(____, ____))