Steigung und Änderungsraten
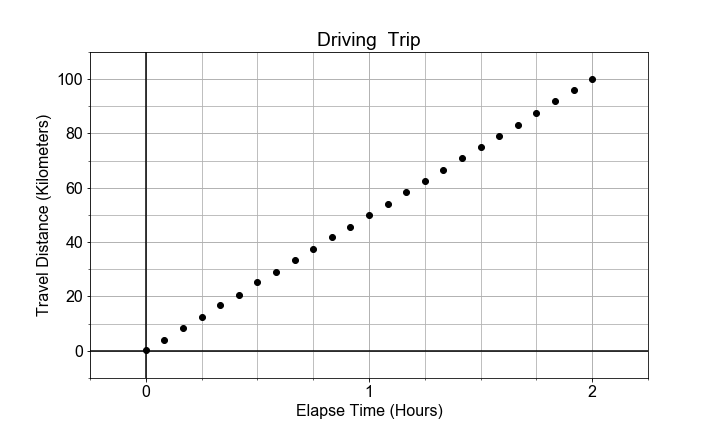
In dieser Übung modellierst du die Bewegung eines Autos mit (ungefähr) konstanter Geschwindigkeit, indem du die durchschnittliche Geschwindigkeit über die gesamte Fahrt berechnest. Die lineare Beziehung wird zwischen der verstrichenen Zeit und der zurückgelegten Strecke modelliert.
In diesem Fall wird der Modellparameter a1, also die Steigung, als mittlere Geschwindigkeit angenähert bzw. „geschätzt“ – anders ausgedrückt: die „Änderungsrate“ der Strecke („rise“) geteilt durch die Zeit („run“).
Diese Übung ist Teil des Kurses
Einführung in lineares Modellieren mit Python
Anleitung zur Übung
- Berechne die punktweisen Differenzen sowohl der
timesals auch derdistancesmitnumpy.diff(). - Berechne ein Array
velocitiesals Quotient ausdiff_distancegeteilt durchdiff_times. - Berechne Mittelwert und Spannweite der Geschwindigkeiten mit den
numpy-Methodenmean,max,min. - Plotte das Array
velocities, um den Durchschnitt und die Streuung der Werte zu visualisieren.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Compute an array of velocities as the slope between each point
diff_distances = np.diff(____)
diff_times = np.diff(____)
velocities = ____ / diff_times
# Chracterize the center and spread of the velocities
v_avg = np.____(velocities)
v_max = np.____(velocities)
v_min = np.____(velocities)
v_range = ____ - ____
# Plot the distribution of velocities
fig = plot_velocity_timeseries(times[1:], velocities)