Schätzung von Populationsparametern
Stell dir eine Konstellation ("Population") von Satelliten vor, die ein ganzes Jahr lang umlaufen, und die in jeder Stunde zurückgelegte Strecke wird in Kilometern gemessen. Zwischen den Stunden gibt es Schwankungen in den gemessenen Distanzen, bedingt durch unbekannte Komplikationen der Orbitaldynamik. Nimm an, wir können nicht alle Daten des Jahres messen, möchten aber ein Populationsmodell für die Schwankungen der stündlichen Orbitdistanz (Geschwindigkeit) auf Basis einer Stichprobe von Messungen erstellen.
In dieser Übung nimmst du an, dass die Population der stündlichen Distanzen am besten durch eine Gauß-Verteilung modelliert wird und zudem, dass die Parameter dieses Populationsmodells aus den Stichprobenstatistiken geschätzt werden können. Starte mit den vorab geladenen sample_distances, die aus einer Population von Satelliten stammen.
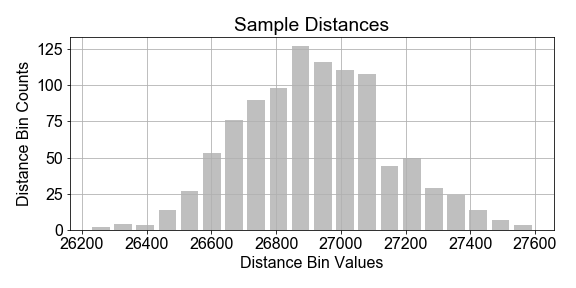
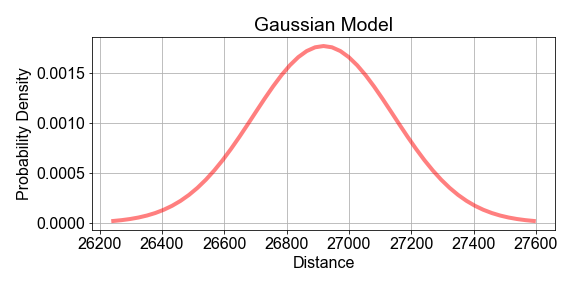
Diese Übung ist Teil des Kurses
Einführung in lineares Modellieren mit Python
Anleitung zur Übung
- Berechne den Mittelwert und die Standardabweichung der
sample_distances. - Verwende die Stichprobenstatistiken
meanundstdevals gute Schätzer für die Parametermuundsigmaeines Populationsmodells. - Übergib diese Werte und
sample_distancesan die vordefinierte Funktiongaussian_model(), um das Populationsmodell zu erstellen. - Verwende die vordefinierte Funktion
plot_model_and_data(), um die Stichprobendaten zusammen mit dem Populationsmodell zu plotten.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Compute the mean and standard deviation of the sample_distances
sample_mean = np.mean(____)
sample_stdev = np.std(____)
# Use the sample mean and stdev as estimates of the population model parameters mu and sigma
population_model = gaussian_model(____, mu=____, sigma=____)
# Plot the model and data to see how they compare
fig = plot_data_and_model(sample_distances, population_model)