Variation um den Trend
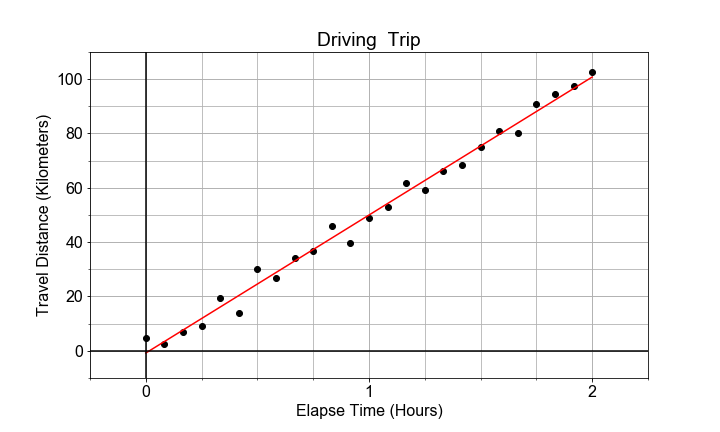
Daten müssen nicht perfekt linear sein; Messungen können zufällige Schwankungen oder eine gewisse „Streuung“ aufweisen. Das führt zu Variation in den Modellparametern. Diese Variation bei einem Parameter wird durch den „Standardfehler“ quantifiziert und als „Unsicherheit“ in der Schätzung des Modellparameters interpretiert.
In dieser Übung verwendest du ols aus statsmodels, um ein Modell zu erstellen und den Standardfehler für jeden Parameter dieses Modells zu extrahieren.
Diese Übung ist Teil des Kurses
Einführung in lineares Modellieren mit Python
Anleitung zur Übung
- Speichere die vorab geladenen Daten in einem DataFrame
dfund benennex_dataalstimesundy_dataalsdistances. - Verwende
model_fit = ols().fit(), um ein lineares Modell der Formformula="distances ~ times"aufdata=dfzu fitten. - Extrahiere den geschätzten Achsenabschnitt
model_fit.params['Intercept']und den Standardfehler des Achsenabschnitts ausmodel_fit.bse['Intercept']. - Wiederhole das für die Steigung und gib anschließend alle 4 Werte mit aussagekräftigen Namen aus.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Store x_data and y_data, as times and distances, in df, and use ols() to fit a model to it.
df = pd.DataFrame(dict(____=x_data, ____=y_data))
model_fit = ols(____="distances ~ times", data=____).____()
# Extact the model parameters and their uncertainties
a0 = model_fit.____['Intercept']
e0 = model_fit.____['Intercept']
a1 = model_fit.____['times']
e1 = model_fit.____['times']
# Print the results with more meaningful names
print('Estimate of the intercept = {:0.2f}'.format(____))
print('Uncertainty of the intercept = {:0.2f}'.format(____))
print('Estimate of the slope = {:0.2f}'.format(____))
print('Uncertainty of the slope = {:0.2f}'.format(____))