R-Quadrat
Zuvor haben wir ein weiteres Gütemaß, R-Quadrat, als Verhältnis von RSS zu VAR ausgedrückt. Multipliziert man Zähler und Nenner dieses Verhältnisses mit 1/n, erhält man eine numerisch äquivalente Form: das Verhältnis der Varianz der Residuen zur Varianz des linearen Trends in den Daten, die wir modellieren. Das lässt sich so interpretieren, dass es misst, wie viel der Varianz in deinen Daten durch dein Modell „erklärt“ wird – im Gegensatz zur Streuung bzw. Varianz der Residuen (nachdem du den linearen Trend entfernt hast).
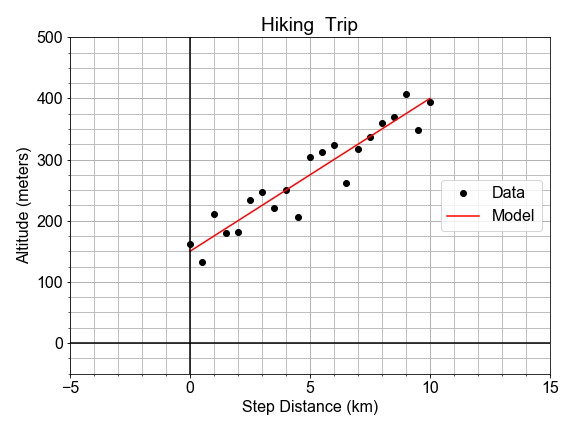
Hier haben wir die Daten x_data, y_data und die Modellvorhersagen y_model für das Best-Fit-Modell bereits geladen; dein Ziel ist es, das R-Quadrat zu berechnen, um zu quantifizieren, wie viel dieses lineare Modell von der Variation in den Daten erfasst.
Diese Übung ist Teil des Kurses
Einführung in lineares Modellieren mit Python
Anleitung zur Übung
- Berechne die
residuals, indem duy_datavony_modelsubtrahierst, und diedeviations, indem duy_datavomnp.mean()dery_datasubtrahierst. - Berechne die Varianz der
residualsund die Varianz derdeviations, jeweils mitnp.mean()undnp.square(). - Berechne
r_squaredals 1 minus dem Verhältnisvar_residuals / var_deviationsund gib das Ergebnis aus.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Compute the residuals and the deviations
residuals = ____ - y_data
deviations = np.____(____) - y_data
# Compute the variance of the residuals and deviations
var_residuals = np.____(np.____(____))
var_deviations = np.____(np.____(____))
# Compute r_squared as 1 - the ratio of RSS/Variance
r_squared = 1 - (____ / ____)
print('R-squared is {:0.2f}'.format(____))