Inferencia para la tendencia posterior
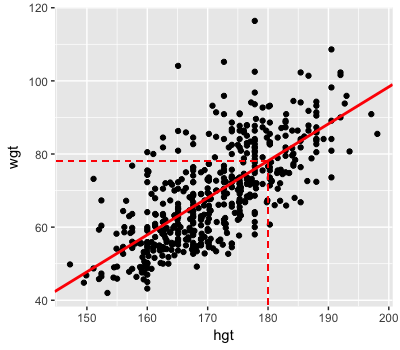
Recuerda la verosimilitud del modelo bayesiano de regresión del peso \(Y\) por altura \(X\): \(Y \sim N(m, s^2)\) donde \(m = a + b X\). En ejercicios anteriores aproximaste la forma de la tendencia posterior \(m\) (línea continua). A partir de esto, observa que el peso típico entre personas adultas de 180 cm es aproximadamente 80 kg (líneas discontinuas):
Usarás la salida de simulación de RJAGS para aproximar la tendencia posterior del peso entre personas adultas de 180 cm, así como la incertidumbre posterior de esta tendencia. La simulación de 100.000 iteraciones de la posterior, weight_sim_big, está en tu espacio de trabajo junto con un data frame con la salida de la cadena de Markov, weight_chains.
Este ejercicio forma parte del curso
Modelado bayesiano con RJAGS
Instrucciones del ejercicio
weight_chainscontiene 100.000 conjuntos de valores plausibles posteriores de los parámetros \(a\) y \(b\). A partir de cada uno, calcula el peso medio (típico) entre personas adultas de 180 cm, \(a + b * 180\). Guarda estas tendencias como una nueva variablem_180enweight_chains.Construye un gráfico de densidad posterior de los 100.000 valores de
m_180.Usa los 100.000 valores de
m_180para calcular un intervalo creíble posterior del 95% para el peso medio entre personas adultas de 180 cm.
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Calculate the trend under each Markov chain parameter set
weight_chains <- weight_chains %>%
mutate(m_180 = ___)
# Construct a posterior density plot of the trend
ggplot(___, aes(x = ___)) +
geom_density()
# Construct a posterior credible interval for the trend
quantile(___, probs = c(___, ___))