Erwartete Anzahl von Zählungen berechnen

In den vorherigen Übungen hast du Mittelwert und Varianz der Crab-Daten berechnet und festgestellt, dass sie nicht gleich sind. In dieser Übung übst du eine weitere Analyse auf Overdispersion, indem du den bereits berechneten Mittelwert nutzt und die erwartete Anzahl der Zählungen für einen bestimmten Zählwert berechnest, zum Beispiel für Nullzählungen. Mit anderen Worten: Welche Anzahl an Null-Satelliten sollten wir in der Stichprobe erwarten, gegeben den berechneten Stichprobenmittelwert?

Erinnere dich an die Abbildung aus dem crab-Datensatz, in der du viele Nullzählungen erkennen kannst.

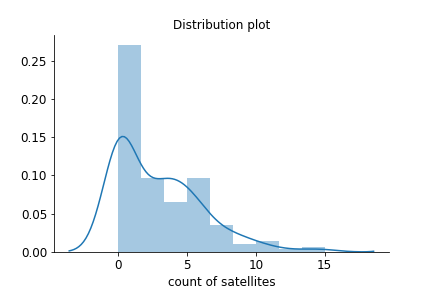
Zur Erinnerung: Um die erwartete Anzahl von Zählungen gegeben den Parameter zu berechnen, kannst du die definierte Poisson-Verteilung verwenden, gegeben durch

$$ P(y)=\frac{\lambda^ye^{-\lambda}}{y!} $$

Der crab-Datensatz und der berechnete Mittelwert sat_mean sind im Workspace vorgeladen.

Diese Übung ist Teil des Kurses

Generalisierte lineare Modelle in Python

Kurs anzeigen

Anleitung zur Übung

Berechne mit dem berechneten Mittelwert sat_mean und den Nullzählungen $y = 0$ die erwartete Anzahl an Nullzählungen. Verwende math factorial().
Ermittle die Anzahl der Beobachtungen mit Nullzählungen in der Variable sat mit sum() und die Gesamtzahl der Beobachtungen in der Stichprobe mit len().
Gib das Verhältnis aus tatsächlichen Nullzählungs-Beobachtungen und Gesamtzahl der Beobachtungen aus.

Interaktive Übung

Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.

# Expected number of zero counts
exp_zero_cnt = ((____**____)*np.____(-____))/math.____(____)

# Print exp_zero_counts
print('Expected zero counts given mean of ', round(____,3), 
      'is ', round(____,3)*100)

# Number of zero counts in sat variable
actual_zero_cnt = sum(____[____]  == 0)

# Number of observations in crab dataset
num_obs = len(____)

# Print the percentage of zero count observations in the sample
print('Actual zero counts in the sample: ', round(____ / ____,3)*100)

Code bearbeiten und ausführen