Änderungsrate der Wahrscheinlichkeit

Für den Datensatz wells hast du bereits ein logistisches Regressionsmodell mit der Modellformel switch ~ distance100 angepasst und dabei die folgende Schätzung erhalten: $$ log(\frac{\mu}{1-\mu}) = 0.6060 - 0.6219\times distance100 $$

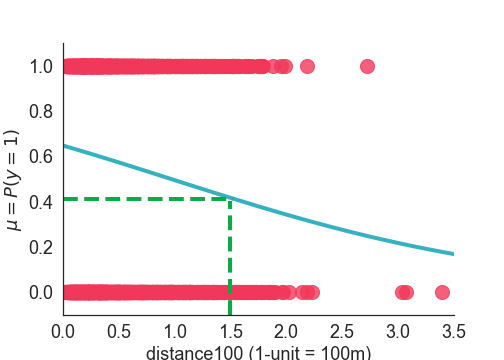
In dieser Übung verwendest du dieses Modell, um zu verstehen, wie sich die geschätzte Wahrscheinlichkeit bei einem bestimmten Wert von distance100 verändert, zum Beispiel bei 1,5, wie in der Abbildung unten dargestellt.

Erinnere dich an die Formeln für die Inverse-Logit-Funktion (Wahrscheinlichkeit)

$$ \mu = \frac{exp(\beta_0+\beta_1x_1)}{1+exp(\beta_0+\beta_1x_1)} $$

und die Steigung der Tangente der Modellanpassung im Punkt \(x\):

$$ \beta*\mu(1-\mu) $$

Der Datensatz wells und das Modell wells_GLM sind im Workspace geladen.