Variation en deux parties
On vous donne deux jeux de données distance-temps : l’un avec une très petite vitesse et l’autre avec une grande vitesse. Remarquez que tous deux peuvent avoir la même erreur standard de pente, mais des R-carré différents pour l’ensemble du modèle, selon la valeur de la pente (« taille d’effet ») comparée à l’erreur standard (« incertitude »).
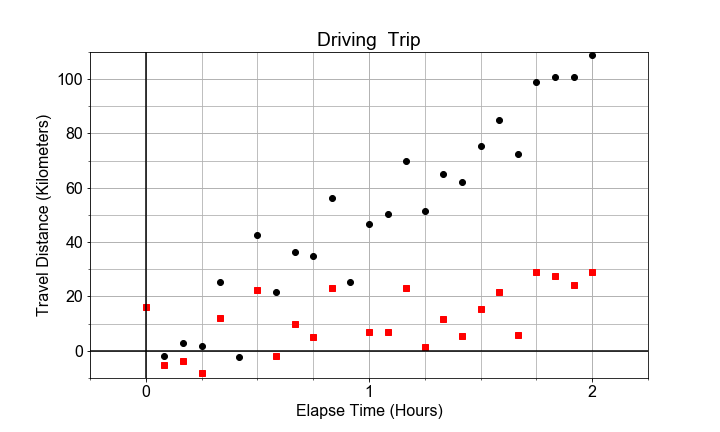
Si l’on trace les deux jeux de données en nuage de points sur les mêmes axes, le contraste est net. La variation due à la pente est différente de la variation due à la dispersion aléatoire autour de la droite de tendance. Dans cet exercice, votre objectif est de calculer l’erreur standard et le R-carré pour deux jeux de données, puis de les comparer.
Cet exercice fait partie du cours
Introduction à la modélisation linéaire en Python
Instructions
- Construisez et
fit()un modèleols()pour les deux jeux de donnéesdistances1etdistances2. - Utilisez la propriété
.bsedes modèles obtenusmodel_1etmodel_2, ainsi que la clé'times', pour extraire la valeur de l’erreur standard de la pente pour chaque modèle. - Utilisez l’attribut
.rsquaredpour extraire la valeur du R-carré de chaque modèle. - Affichez
se_1,rsquared_1,se_2,rsquared_2, puis comparez visuellement.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Build and fit two models, for columns distances1 and distances2 in df
model_1 = ols(formula="____ ~ times", data=df).____()
model_2 = ols(formula="____ ~ times", data=df).____()
# Extract R-squared for each model, and the standard error for each slope
se_1 = model_1.____['times']
se_2 = model_2.____['times']
rsquared_1 = model_1.____
rsquared_2 = model_2.____
# Print the results
print('Model 1: SE = {:0.3f}, R-squared = {:0.3f}'.format(____, ____))
print('Model 2: SE = {:0.3f}, R-squared = {:0.3f}'.format(____, ____))