Estimation des paramètres de la population

Imaginez une constellation (« population ») de satellites en orbite pendant une année complète, et la distance parcourue chaque heure est mesurée en kilomètres. Il existe une variation d’une heure à l’autre dans les distances mesurées, due à des complications inconnues de la dynamique orbitale. Supposons que vous ne puissiez pas mesurer toutes les données de l’année, mais que vous souhaitiez construire un modèle de population pour les variations de distance orbitale par heure (vitesse) à partir d’un échantillon de mesures.

Dans cet exercice, vous supposerez que la population des distances horaires est mieux modélisée par une loi gaussienne, et vous supposerez en outre que les paramètres de ce modèle de population peuvent être estimés à partir des statistiques de l’échantillon. Commencez avec sample_distances, préchargé, prélevé sur une population de satellites.

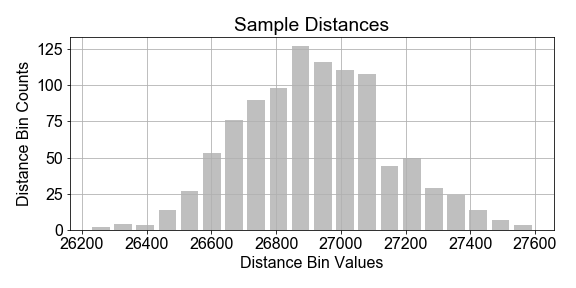
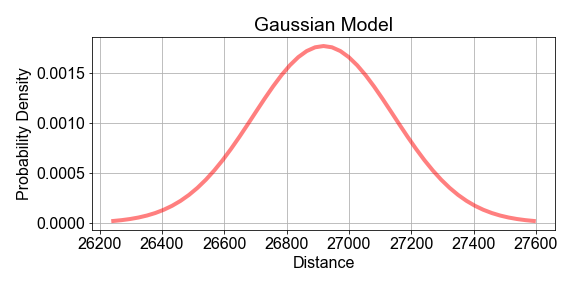
Cet exercice fait partie du cours

Introduction à la modélisation linéaire en Python

Afficher le cours

Instructions

Calculez la moyenne et l’écart type de sample_distances.
Utilisez les statistiques d’échantillon, mean et stdev, comme bonnes estimations des paramètres mu et sigma d’un modèle de population.
Passez ces valeurs, ainsi que sample_distances, à la fonction gaussian_model() prédéfinie pour construire le modèle de population.
Utilisez plot_model_and_data() (prédéfini) pour tracer ensemble l’échantillon et le modèle de population.

Exercice interactif pratique

Essayez cet exercice en complétant cet exemple de code.

# Compute the mean and standard deviation of the sample_distances
sample_mean = np.mean(____)
sample_stdev = np.std(____)

# Use the sample mean and stdev as estimates of the population model parameters mu and sigma
population_model = gaussian_model(____, mu=____, sigma=____)

# Plot the model and data to see how they compare
fig = plot_data_and_model(sample_distances, population_model)

Modifier et exécuter le code

Cet exercice fait partie du cours

Introduction à la modélisation linéaire en Python

IntermédiaireNiveau de compétence

4.8+

Commencer le cours gratuitement

Nous commençons le cours par une exploration des relations linéaires, avec des exemples concrets illustrant l’usage des modèles linéaires et des démonstrations de méthodes de visualisation de données avec matplotlib. Nous utilisons ensuite des statistiques descriptives pour quantifier la forme de nos données et la corrélation pour mesurer l’intensité des relations linéaires entre deux variables.

Exercise 1: Introduction à la modélisation des données Exercise 2: Pourquoi modéliser : interpolation Exercise 3: Pourquoi modéliser : extrapolation Exercise 4: Pourquoi modéliser : estimer des relations Exercise 5: Visualiser des relations linéaires Exercise 6: Tracer les données Exercise 7: Tracer le modèle sur les données Exercise 8: Estimer visuellement la pente et l’ordonnée à l’origine Exercise 9: Quantifier les relations linéaires Exercise 10: Moyenne, écart et écart type Exercise 11: Covariance vs Corrélation Exercise 12: Force de la corrélation

Nous examinons ici les éléments qui composent un modèle linéaire. En nous appuyant sur l’idée de série de Taylor, nous nous concentrons sur les paramètres pente et intercept, sur la façon dont ils définissent le modèle et comment les interpréter dans plusieurs contextes appliqués. Nous utilisons différents modules Python pour trouver le modèle qui s’ajuste le mieux aux données, en calculant les valeurs optimales de la pente et de l’intercept, à l’aide des moindres carrés, de numpy, de statsmodels et de scikit-learn.

Exercise 1: Qu’est-ce qui fait qu’un modèle est linéaire Exercise 2: Termes d’un modèle Exercise 3: Composants du modèle Exercise 4: Paramètres du modèle Exercise 5: Interpréter la pente et l’ordonnée à l’origine Exercise 6: Proportionnalité linéaire Exercise 7: Pente et taux de variation Exercise 8: Ordonnée à l’origine et points de départ Exercise 9: Optimisation du modèle Exercise 10: Somme des carrés des résidus Exercise 11: Minimiser les résidus Exercise 12: Visualiser les minima du RSS Exercise 13: Optimisation aux moindres carrés Exercise 14: Moindres carrés avec `numpy`Exercise 15: Optimisation avec SciPy Exercise 16: Moindres carrés avec `statsmodels`

Nous allons ensuite appliquer des modèles à des données réelles et réaliser des prédictions. Nous explorerons certaines des limites et écueils courants des prédictions, puis nous évaluerons et comparerons des modèles en quantifiant et contrastant plusieurs mesures d’ajustement, notamment la RMSE et le R-carré.

Exercise 1: Modéliser des données réelles Exercise 2: Modèle linéaire en anthropologie Exercise 3: Modèle linéaire en océanographie Exercise 4: Modèle linéaire en cosmologie Exercise 5: Les limites de la prédiction Exercise 6: Interpolation : entre deux dates Exercise 7: Extrapolation : franchir la limite Exercise 8: Qualité de l’ajustement Exercise 9: RMSE étape par étape Exercise 10: R carré Exercise 11: Erreur standard Exercise 12: Variation autour de la tendance Exercise 13: Variation en deux parties

Dans le dernier chapitre, nous introduisons des notions de statistiques inférentielles et nous les utilisons pour montrer comment l’estimation du maximum de vraisemblance et le bootstrap peuvent servir à estimer les paramètres d’un modèle linéaire. Nous appliquerons ensuite ces méthodes pour formuler des affirmations probabilistes sur notre confiance dans les paramètres du modèle.

Exercise 1: Notions de statistique inférentielle Exercise 2: Statistiques d'échantillon versus population Exercise 3: Variation des statistiques d’échantillon Exercise 4: Visualiser la variabilité d’une statistique Exercise 5: Estimation du modèle et vraisemblance Exercise 6: Estimation des paramètres de la population

Exercice en cours

Exercise 7: Maximiser la vraisemblance, partie 1 Exercise 8: Maximiser la vraisemblance, partie 2 Exercise 9: Incertitude du modèle et distributions d’échantillonnage Exercise 10: Bootstrap et erreur standard Exercise 11: Estimation de la vitesse et de la confiance Exercise 12: Visualiser le bootstrap Exercise 13: Erreurs de modèle et aléa Exercise 14: Statistiques de test et taille d’effet Exercise 15: Hypothèse nulle Exercise 16: Visualiser des statistiques de test Exercise 17: Visualiser la valeur p Exercise 18: Conclusion du cours