Estimer visuellement la pente et l’ordonnée à l’origine

Construire des modèles linéaires automatise une démarche que l’on peut approximativement faire « à la main » avec de la visualisation et beaucoup d’essais-erreurs. Cette méthode visuelle n’est ni la plus efficace ni la plus précise, mais elle illustre très bien les concepts, alors essayons !

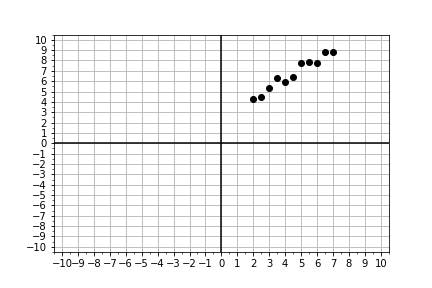
À partir de données mesurées, votre objectif est d’estimer une valeur pour la pente et l’ordonnée à l’origine, de les passer au modèle, puis d’ajuster votre estimation jusqu’à ce que le modèle s’aligne sur les données. Utilisez les données fournies xd, yd et la fonction model() fournie pour créer des prédictions du modèle. Comparez les prédictions et les données avec plot_data_and_model() fournie.

Cet exercice fait partie du cours

Introduction à la modélisation linéaire en Python

Afficher le cours

Instructions

Examinez le graphique ci-dessus et proposez des estimations préliminaires pour trial_slope et trial_intercept. Vous pourrez les ajuster ensuite dans l’exercice.
Utilisez la fonction prédéfinie xm, ym = model(intercept, slope) pour générer les prédictions du modèle.
Utilisez la fonction fournie fig = plot_data_and_model(xd, yd, xm, ym) pour tracer ensemble les données mesurées (xd, yd) et les prédictions du modèle (xm, ym).
Si le modèle n’ajuste pas bien les données, essayez d’autres valeurs pour trial_slope et trial_intercept puis relancez votre code.
Répétez jusqu’à obtenir, selon vous, les meilleures valeurs, puis assignez-les à final_slope et final_intercept et Soumettre la réponse.

Exercice interactif pratique

Essayez cet exercice en complétant cet exemple de code.

# Look at the plot data and guess initial trial values
trial_slope = ____
trial_intercept = ____

# input thoses guesses into the model function to compute the model values.
xm, ym = ____(trial_intercept, trial_slope)

# Compare your your model to the data with the plot function
fig = ____(xd, yd, xm, ym)
plt.show()

# Repeat the steps above until your slope and intercept guess makes the model line up with the data.
final_slope = ____
final_intercept = ____

Modifier et exécuter le code

Cet exercice fait partie du cours

Introduction à la modélisation linéaire en Python

IntermédiaireNiveau de compétence

4.8+

Commencer le cours gratuitement

Nous commençons le cours par une exploration des relations linéaires, avec des exemples concrets illustrant l’usage des modèles linéaires et des démonstrations de méthodes de visualisation de données avec matplotlib. Nous utilisons ensuite des statistiques descriptives pour quantifier la forme de nos données et la corrélation pour mesurer l’intensité des relations linéaires entre deux variables.

Exercise 1: Introduction à la modélisation des données Exercise 2: Pourquoi modéliser : interpolation Exercise 3: Pourquoi modéliser : extrapolation Exercise 4: Pourquoi modéliser : estimer des relations Exercise 5: Visualiser des relations linéaires Exercise 6: Tracer les données Exercise 7: Tracer le modèle sur les données Exercise 8: Estimer visuellement la pente et l’ordonnée à l’origine

Exercice en cours

Exercise 9: Quantifier les relations linéaires Exercise 10: Moyenne, écart et écart type Exercise 11: Covariance vs Corrélation Exercise 12: Force de la corrélation

Nous examinons ici les éléments qui composent un modèle linéaire. En nous appuyant sur l’idée de série de Taylor, nous nous concentrons sur les paramètres pente et intercept, sur la façon dont ils définissent le modèle et comment les interpréter dans plusieurs contextes appliqués. Nous utilisons différents modules Python pour trouver le modèle qui s’ajuste le mieux aux données, en calculant les valeurs optimales de la pente et de l’intercept, à l’aide des moindres carrés, de numpy, de statsmodels et de scikit-learn.

Exercise 1: Qu’est-ce qui fait qu’un modèle est linéaire Exercise 2: Termes d’un modèle Exercise 3: Composants du modèle Exercise 4: Paramètres du modèle Exercise 5: Interpréter la pente et l’ordonnée à l’origine Exercise 6: Proportionnalité linéaire Exercise 7: Pente et taux de variation Exercise 8: Ordonnée à l’origine et points de départ Exercise 9: Optimisation du modèle Exercise 10: Somme des carrés des résidus Exercise 11: Minimiser les résidus Exercise 12: Visualiser les minima du RSS Exercise 13: Optimisation aux moindres carrés Exercise 14: Moindres carrés avec `numpy`Exercise 15: Optimisation avec SciPy Exercise 16: Moindres carrés avec `statsmodels`

Nous allons ensuite appliquer des modèles à des données réelles et réaliser des prédictions. Nous explorerons certaines des limites et écueils courants des prédictions, puis nous évaluerons et comparerons des modèles en quantifiant et contrastant plusieurs mesures d’ajustement, notamment la RMSE et le R-carré.

Exercise 1: Modéliser des données réelles Exercise 2: Modèle linéaire en anthropologie Exercise 3: Modèle linéaire en océanographie Exercise 4: Modèle linéaire en cosmologie Exercise 5: Les limites de la prédiction Exercise 6: Interpolation : entre deux dates Exercise 7: Extrapolation : franchir la limite Exercise 8: Qualité de l’ajustement Exercise 9: RMSE étape par étape Exercise 10: R carré Exercise 11: Erreur standard Exercise 12: Variation autour de la tendance Exercise 13: Variation en deux parties

Dans le dernier chapitre, nous introduisons des notions de statistiques inférentielles et nous les utilisons pour montrer comment l’estimation du maximum de vraisemblance et le bootstrap peuvent servir à estimer les paramètres d’un modèle linéaire. Nous appliquerons ensuite ces méthodes pour formuler des affirmations probabilistes sur notre confiance dans les paramètres du modèle.

Exercise 1: Notions de statistique inférentielle Exercise 2: Statistiques d'échantillon versus population Exercise 3: Variation des statistiques d’échantillon Exercise 4: Visualiser la variabilité d’une statistique Exercise 5: Estimation du modèle et vraisemblance Exercise 6: Estimation des paramètres de la population Exercise 7: Maximiser la vraisemblance, partie 1 Exercise 8: Maximiser la vraisemblance, partie 2 Exercise 9: Incertitude du modèle et distributions d’échantillonnage Exercise 10: Bootstrap et erreur standard Exercise 11: Estimation de la vitesse et de la confiance Exercise 12: Visualiser le bootstrap Exercise 13: Erreurs de modèle et aléa Exercise 14: Statistiques de test et taille d’effet Exercise 15: Hypothèse nulle Exercise 16: Visualiser des statistiques de test Exercise 17: Visualiser la valeur p Exercise 18: Conclusion du cours