Force de la corrélation
De manière intuitive, on peut regarder les graphiques fournis et « voir » si les deux variables semblent « varier ensemble ».
- Jeu de données A : x et y évoluent ensemble et semblent avoir une relation forte.
- Jeu de données B : tendance générale à la hausse ; x et y ne sont que faiblement liés.
- Jeu de données C : ressemble à un nuage aléatoire ; x et y ne semblent pas varier ensemble et sont indépendants.
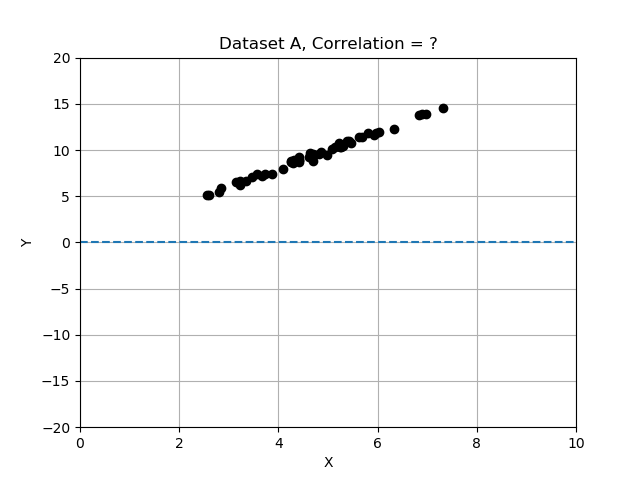
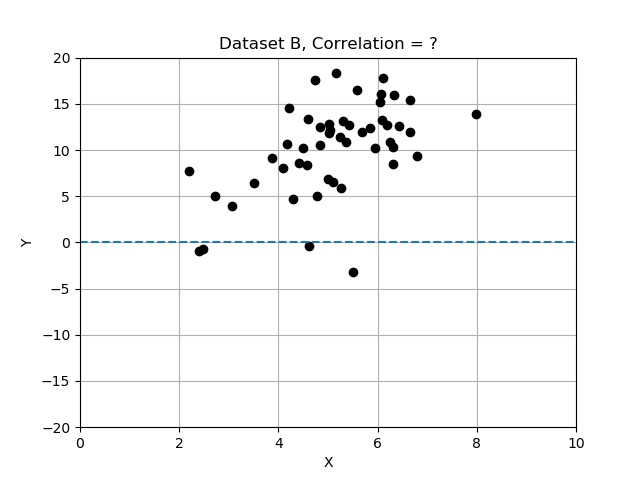
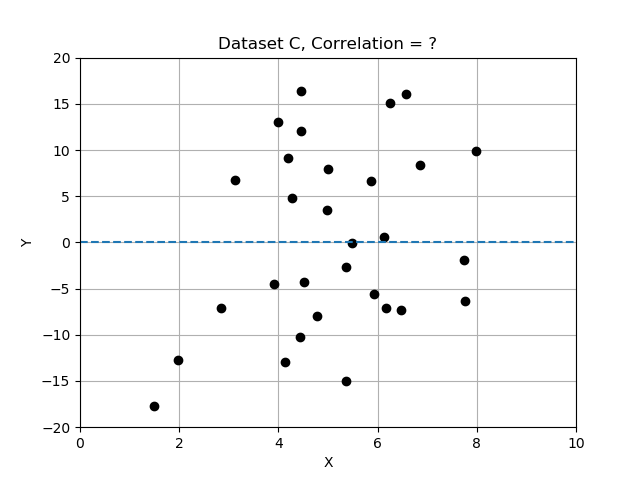
Rappelez-vous que les écarts diffèrent de la moyenne et que nous les avons normalisés en divisant les écarts par l’écart type. Dans cet exercice, vous allez comparer les 3 jeux de données en calculant la corrélation et en déterminant lequel présente les variables x et y les plus fortement corrélées. Utilisez la table de données fournie data_sets, un dictionnaire d’enregistrements, chacun avec les clés 'name', 'x', 'y' et 'correlation'.
Cet exercice fait partie du cours
Introduction à la modélisation linéaire en Python
Instructions
- Complétez la définition de la fonction
correlation()à l’aide de la moyenne des produits des écarts normalisés dexety. - Itérez sur
data_sets, calculez et stockez chaque corrélation aveccorrelation(record['x'], record['y']). - Exécutez le code jusqu’à ce point (c’est-à-dire jusqu’à la fin de la boucle for) et inspectez l’affichage. Quel jeu de données présente la corrélation la plus forte ?
- Affectez le nom du jeu de données (
data_sets['A'],data_sets['B']oudata_sets['C']) ayant la corrélation la plus forte à la variablebest_data.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Complete the function that will compute correlation.
def correlation(x,y):
x_dev = x - np.____(x)
y_dev = y - np.____(y)
x_norm = x_dev / np.____(x)
y_norm = y_dev / np.____(y)
return np.____(x_norm * y_norm)
# Compute and store the correlation for each data set in the list.
for name, data in data_sets.items():
data['correlation'] = ____(data['x'], data['y'])
print('data set {} has correlation {:.2f}'.format(name, data['correlation']))
# Assign the data set with the best correlation.
best_data = data_sets['____']