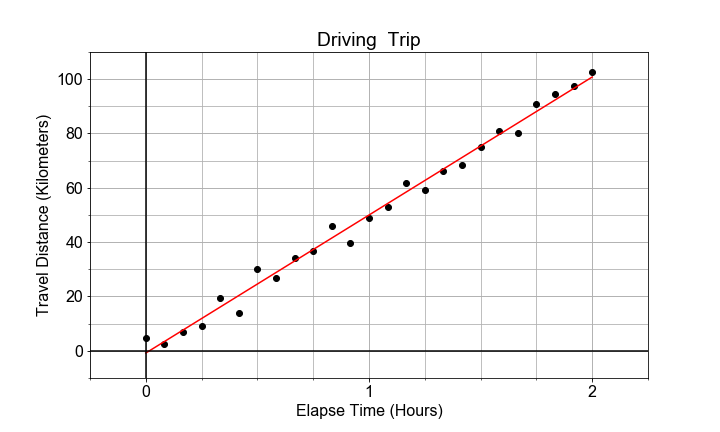
Variation autour de la tendance
Les données n’ont pas besoin d’être parfaitement linéaires, et il peut y avoir une variation aléatoire ou un « étalement » dans les mesures, ce qui se traduit par une variation des paramètres du modèle. Cette variation d’un paramètre est quantifiée par l’« erreur standard », et s’interprète comme une « incertitude » sur l’estimation du paramètre du modèle.
Dans cet exercice, vous allez utiliser ols de statsmodels pour construire un modèle et extraire l’erreur standard de chacun de ses paramètres.
Cet exercice fait partie du cours
Introduction à la modélisation linéaire en Python
Instructions
- Stockez les données préchargées dans un DataFrame
df, en renommantx_dataentimesety_dataendistances. - Utilisez
model_fit = ols().fit()pour ajuster un modèle linéaire de la formeformula="distances ~ times"auxdata=df. - Extrayez l’ordonnée à l’origine estimée avec
model_fit.params['Intercept']et l’erreur standard de l’ordonnée à l’origine avecmodel_fit.bse['Intercept']. - Recommencez pour la pente, puis affichez les 4 valeurs avec des noms explicites.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Store x_data and y_data, as times and distances, in df, and use ols() to fit a model to it.
df = pd.DataFrame(dict(____=x_data, ____=y_data))
model_fit = ols(____="distances ~ times", data=____).____()
# Extact the model parameters and their uncertainties
a0 = model_fit.____['Intercept']
e0 = model_fit.____['Intercept']
a1 = model_fit.____['times']
e1 = model_fit.____['times']
# Print the results with more meaningful names
print('Estimate of the intercept = {:0.2f}'.format(____))
print('Uncertainty of the intercept = {:0.2f}'.format(____))
print('Estimate of the slope = {:0.2f}'.format(____))
print('Uncertainty of the slope = {:0.2f}'.format(____))