La nature récursive de la variance GARCH
Selon l’équation GARCH(1,1), la variance prédite dépend de la surprise au carré sur le rendement et de la prédiction de variance précédente :
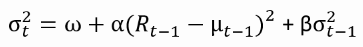
Vous pouvez l’implémenter à l’aide d’une boucle (reportez-vous au diaporama si vous ne vous souvenez plus de la structure de boucle vue dans la vidéo).
Faisons cela pour les rendements quotidiens du S&P 500. Les variables omega, alpha, beta, nobs, e2 et predvar sont déjà chargées dans votre environnement R.
Cet exercice fait partie du cours
Modèles GARCH en R
Instructions
- Calculez les variances prédites.
- Utilisez
predvarpour définir la série de volatilité annualisée préditeann_predvol. - Tracez la volatilité annualisée prédite pour les années 2008-2009 afin d’observer la dynamique autour de la crise financière.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Compute the predicted variances
predvar[1] <- var(sp500ret)
for(t in 2:nobs){
predvar[t] <- ___ + ___ * e2[t-1] + ___ * predvar[___]
}
# Create annualized predicted volatility
ann_predvol <- xts(___(252) * sqrt(___), order.by = time(sp500ret))
# Plot the annual predicted volatility in 2008 and 2009
___(___["2008::2009"], main = "Ann. S&P 500 vol in 2008-2009")