La dynamique AR(1)-GJR GARCH des rendements MSFT
Vous avez vu dans la vidéo que le signe du paramètre autorégressif dans le modèle AR(1) dépend de la réaction du marché aux nouvelles
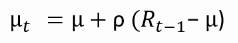
Une valeur positive de \(\rho\) correspond à l’idée que les marchés sous-réagissent aux nouvelles, ce qui engendre un effet de momentum dans les rendements. Une valeur négative de \(\rho\) correspond à l’idée que les marchés sur-réagissent aux nouvelles, ce qui engendre un effet de retour à la moyenne dans les rendements.
Les rendements quotidiens de Microsoft présentent-ils un effet de momentum ou de retournement dans leur dynamique AR(1) ? Découvrons-le en estimant les paramètres du modèle AR(1)-GJR GARCH à l’aide des rendements quotidiens de Microsoft dans msftret.
Cet exercice fait partie du cours
Modèles GARCH en R
Instructions
armaOrder = c(1,2)correspond à un modèle ARMA(1,2). Un modèle AR(1) est équivalent à ARMA(1,0).- Complétez l’argument
mean.modeldansugarchspecpour spécifier le modèle AR(1) à utiliser. - Estimez le modèle.
- Affichez les deux premiers coefficients du modèle GARCH estimé.
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Specify AR(1)-GJR GARCH model
garchspec <- ugarchspec(mean.model = list(armaOrder = ___ ),
variance.model = list(model = "gjrGARCH"),
distribution.model = "sstd")
# Estimate the model
garchfit <- ___
# Print the first two coefficients
___(___)[c(1:2)]