Extrapolación: más allá del límite

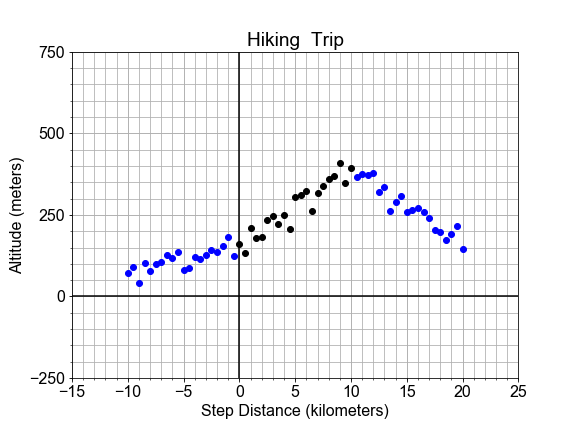
En este ejercicio, vamos a considerar los peligros de la extrapolación. Aquí se muestra el perfil de una ruta de senderismo en una montaña. Un tramo de la ruta, marcado en negro, parece lineal y se usó para construir un modelo. Pero vemos que la recta de mejor ajuste, en rojo, no ajusta fuera del "dominio" original, ya que se extiende hacia estos nuevos datos externos, marcados en azul.

Si queremos usar el modelo para predecir la altitud, pero seguir siendo precisos dentro de cierta tolerancia, ¿cuáles son los valores más pequeños y más grandes de la variable independiente x a los que podemos permitirnos aplicar el modelo?

Aquí, usa las variables precargadas x_data, y_data, y_model y plot_data_model_tolerance() para completar tu solución.

Este ejercicio forma parte del curso

Introducción al modelado lineal en Python

Ver curso

Instrucciones del ejercicio

Usa np.abs() para calcular los residuales como las diferencias y_data - y_model.
Encuentra los valores .min() y .max() de x en los que los residuals son menores que una tolerance = 100 metros.
Usa np.min() y np.max() para imprimir el rango (el mayor y el menor) de valores de x_good.
Usa la función predefinida plot_data_model_tolerance() para comparar los datos, el modelo y el rango de valores de x_good donde residuals < tolerance es True.

Ejercicio interactivo práctico

Prueba este ejercicio y completa el código de muestra.

# Compute the residuals, "data - model", and determine where [residuals < tolerance]
residuals = np.abs(____ - ____)
tolerance = 100
x_good = x_data[____ < ____]

# Find the min and max of the "good" values, and plot y_data, y_model, and the tolerance range
print('Minimum good x value = {}'.format(np.____(____)))
print('Maximum good x value = {}'.format(np.____(____)))
fig = plot_data_model_tolerance(x_data, y_data, y_model, tolerance)

Editar y ejecutar código