Pendiente y tasas de cambio
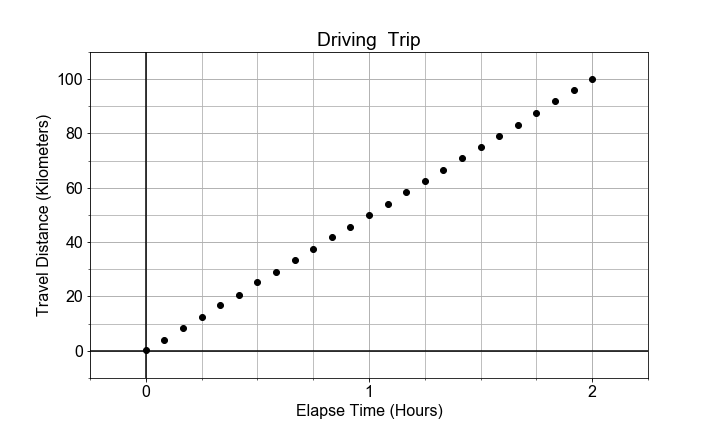
En este ejercicio, vas a modelar el movimiento de un coche que circula a velocidad (aproximadamente) constante calculando la velocidad media durante todo el trayecto. La relación lineal que se modela es entre el tiempo transcurrido y la distancia recorrida.
En este caso, el parámetro del modelo a1, o pendiente, se aproxima o «estima» como la velocidad media; dicho de otro modo, la «tasa de cambio» de la distancia («rise») dividida por el tiempo («run»).
Este ejercicio forma parte del curso
Introducción al modelado lineal en Python
Instrucciones del ejercicio
- Calcula las diferencias punto a punto de
timesydistancesusandonumpy.diff(). - Calcula un array de
velocitiescomo el cociente dediff_distancedividido pordiff_times. - Calcula la media y el rango de valores de velocidad usando los métodos de
numpymean,max,min. - Representa el array
velocitiespara visualizar la media y la dispersión de los valores.
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Compute an array of velocities as the slope between each point
diff_distances = np.diff(____)
diff_times = np.diff(____)
velocities = ____ / diff_times
# Chracterize the center and spread of the velocities
v_avg = np.____(velocities)
v_max = np.____(velocities)
v_min = np.____(velocities)
v_range = ____ - ____
# Plot the distribution of velocities
fig = plot_velocity_timeseries(times[1:], velocities)