Proporcionalidad lineal
La definición de las escalas de temperatura está relacionada con la dilatación lineal de ciertos líquidos, como el mercurio y el alcohol. Originalmente, estas escalas eran literalmente reglas para medir la longitud del fluido en un tubo estrecho marcado o "graduado" como indicador de la temperatura. El alcohol comienza en un bulbo y se expande linealmente hacia el tubo en respuesta al aumento de la temperatura del bulbo o de lo que lo rodea.
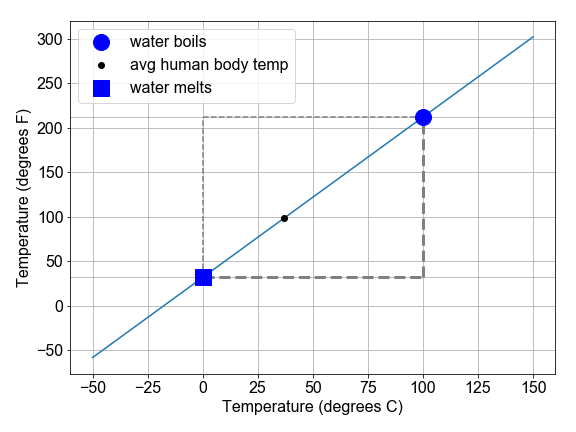
En este ejercicio, exploraremos la conversión entre las escalas Fahrenheit y Celsius como demostración de cómo interpretar la pendiente y la intersección (intercepto) de una relación lineal en un contexto físico.
Este ejercicio forma parte del curso
Introducción al modelado lineal en Python
Instrucciones del ejercicio
- Completa la función
temps_F = convert_scale(temps_C)como un modelo lineal donde "x" estemps_Ce "y" estemps_F. - Calcula el cambio de temperatura en ambas escalas restando la temperatura de congelación de la de ebullición.
- Calcula la
slopecomochange_in_Fdividido entrechange_in_C. - Calcula la
interceptcomo la diferencia entre los puntos de congelaciónfreeze_Fyfreeze_C. - Usa la función predefinida
plot_temperatures()para trazar el modelo resultante.
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Complete the function to convert C to F
def convert_scale(temps_C):
(freeze_C, boil_C) = (0, 100)
(freeze_F, boil_F) = (32, 212)
change_in_C = ____ - freeze_C
change_in_F = ____ - freeze_F
slope = ____ / ____
intercept = ____ - freeze_C
temps_F = ____ + (____ * temps_C)
return temps_F
# Use the convert function to compute values of F and plot them
temps_C = np.linspace(0, 100, 101)
temps_F = convert_scale(temps_C)
fig = plot_temperatures(temps_C, temps_F)