Variación en dos partes

Dados dos conjuntos de datos de distancia frente a tiempo, uno con velocidad muy pequeña y otro con velocidad grande. Observa que ambos pueden tener el mismo error estándar de la pendiente, pero distinto R-squared para el modelo en conjunto, según el tamaño de la pendiente ("tamaño del efecto") en comparación con el error estándar ("incertidumbre").

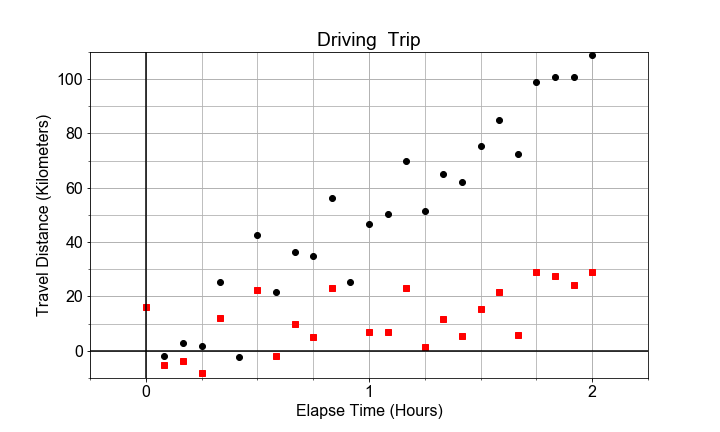
Si representamos ambos conjuntos como diagramas de dispersión en los mismos ejes, el contraste es claro. La variación debida a la pendiente es distinta de la variación debida a la dispersión aleatoria alrededor de la línea de tendencia. En este ejercicio, tu objetivo es calcular el error estándar y el R-squared para ambos conjuntos de datos y compararlos.

Este ejercicio forma parte del curso

Introducción al modelado lineal en Python

Ver curso

Instrucciones del ejercicio

Construye y fit() un modelo ols() para ambos conjuntos de datos, distances1 y distances2.
Usa .bse de los modelos resultantes model_1 y model_2, y la clave 'times' para extraer los valores del error estándar de la pendiente de cada modelo.
Usa el atributo .rsquared para extraer el valor de R-squared de cada modelo.
Imprime los resultados se_1, rsquared_1, se_2, rsquared_2 y compáralos visualmente.

Ejercicio interactivo práctico

Prueba este ejercicio y completa el código de muestra.

# Build and fit two models, for columns distances1 and distances2 in df
model_1 = ols(formula="____ ~ times", data=df).____()
model_2 = ols(formula="____ ~ times", data=df).____()

# Extract R-squared for each model, and the standard error for each slope
se_1 = model_1.____['times']
se_2 = model_2.____['times']
rsquared_1 = model_1.____
rsquared_2 = model_2.____

# Print the results
print('Model 1: SE = {:0.3f}, R-squared = {:0.3f}'.format(____, ____))
print('Model 2: SE = {:0.3f}, R-squared = {:0.3f}'.format(____, ____))

Editar y ejecutar código