Estimación visual de la pendiente e intercepto
Crear modelos lineales es una forma automatizada de hacer algo que podemos hacer de forma aproximada "manualmente" con visualización de datos y mucha prueba y error. El método visual no es el más eficiente ni el más preciso, pero sí ilustra muy bien los conceptos, ¡así que probémoslo!
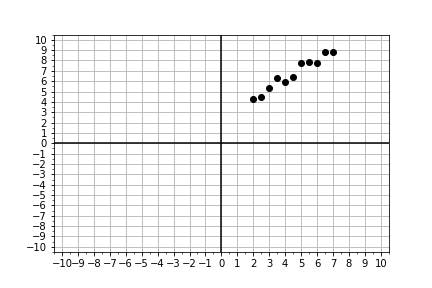
Dados algunos datos medidos, tu objetivo es proponer valores para la pendiente y el intercepto, pasarlos al modelo y ajustar tu propuesta hasta que el modelo resultante se ajuste a los datos. Usa los datos proporcionados xd, yd y la función model() para crear predicciones del modelo. Compara las predicciones y los datos con la función plot_data_and_model() proporcionada.
Este ejercicio forma parte del curso
Introducción al modelado lineal en Python
Instrucciones del ejercicio
- Examina el gráfico de arriba y proporciona estimaciones preliminares de
trial_slopeytrial_intercept. Podrás ajustarlas más adelante en el ejercicio. - Usa la función predefinida
xm, ym = model(intercept, slope)para generar predicciones del modelo. - Usa la función proporcionada
fig = plot_data_and_model(xd, yd, xm, ym)para representar juntos los datos medidos(xd, yd)y las predicciones del modelo(xm, ym). - Si el modelo no se ajusta a los datos, prueba valores distintos para
trial_slopeytrial_intercepty vuelve a ejecutar tu código. - Repite hasta que creas que tienes los mejores valores y, entonces, asígnalos a
final_slopeyfinal_intercepty Enviar respuesta.
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Look at the plot data and guess initial trial values
trial_slope = ____
trial_intercept = ____
# input thoses guesses into the model function to compute the model values.
xm, ym = ____(trial_intercept, trial_slope)
# Compare your your model to the data with the plot function
fig = ____(xd, yd, xm, ym)
plt.show()
# Repeat the steps above until your slope and intercept guess makes the model line up with the data.
final_slope = ____
final_intercept = ____