Covarianza vs correlación
La covarianza mide si dos variables cambian ("varían") juntas. Se calcula obteniendo, punto por punto, los productos de las desviaciones vistas en el ejercicio anterior, dx[n]*dy[n], y luego hallando el promedio de todos esos productos.
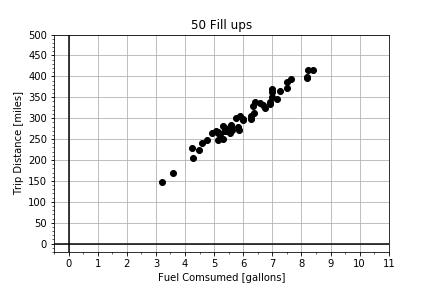
La correlación es, en esencia, la covarianza normalizada. En este ejercicio, se te proporcionan dos arrays de datos que están muy correlacionados, y visualizarás y calcularás tanto la covariance como la correlation.
Este ejercicio forma parte del curso
Introducción al modelado lineal en Python
Instrucciones del ejercicio
- Calcula las desviaciones,
dxydy, restando la media connp.mean(), y calculacovariancecomo la media de su productodx*dy. - Calcula las desviaciones normalizadas,
zxyzy, dividiendo por la desviación estándar connp.std(), y calcula lacorrelationcomo la media de su producto,zx*zy. - Usa
plot_normalized_deviations(zx, zy)para representar el producto de las desviaciones normalizadas y comprobar visualmente que coincide con el valor de la correlación.
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Compute the covariance from the deviations.
dx = x - np.____(x)
dy = y - np.____(y)
covariance = np.____(____ * ____)
print("Covariance: ", covariance)
# Compute the correlation from the normalized deviations.
zx = dx / np.____(x)
zy = dy / np.____(y)
correlation = np.____(____ * ____)
print("Correlation: ", correlation)
# Plot the normalized deviations for visual inspection.
fig = plot_normalized_deviations(zx, zy)