Variación alrededor de la tendencia

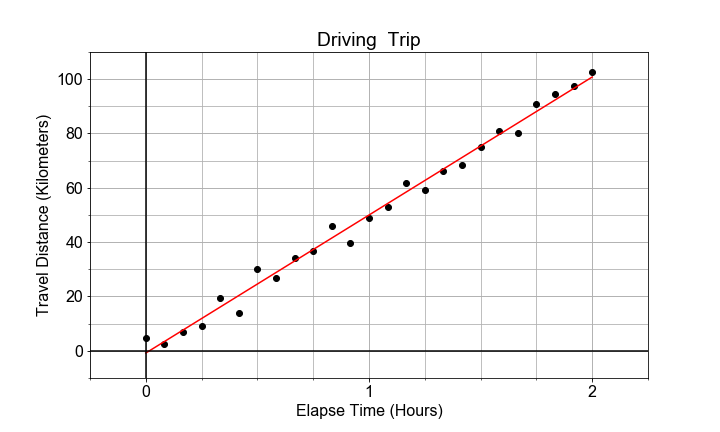
Los datos no tienen por qué ser perfectamente lineales, y puede haber cierta variación aleatoria o «dispersión» en las mediciones, lo que se traduce en variación de los parámetros del modelo. Esta variación en el parámetro se cuantifica mediante el «error estándar» y se interpreta como la «incertidumbre» en la estimación del parámetro del modelo.

En este ejercicio, usarás ols de statsmodels para construir un modelo y extraer el error estándar de cada parámetro de ese modelo.

Este ejercicio forma parte del curso

Introducción al modelado lineal en Python

Ver curso

Instrucciones del ejercicio

Guarda los datos precargados en un DataFrame df, etiquetando x_data como times y y_data como distances.
Usa model_fit = ols().fit() para ajustar un modelo lineal de la forma formula="distances ~ times" con data=df.
Extrae la intercepción estimada con model_fit.params['Intercept'] y el error estándar correspondiente desde model_fit.bse['Intercept'].
Repite para la pendiente y luego imprime los 4 valores con nombres descriptivos.

Ejercicio interactivo práctico

Prueba este ejercicio y completa el código de muestra.

# Store x_data and y_data, as times and distances, in df, and use ols() to fit a model to it.
df = pd.DataFrame(dict(____=x_data, ____=y_data))
model_fit = ols(____="distances ~ times", data=____).____()

# Extact the model parameters and their uncertainties
a0 = model_fit.____['Intercept']
e0 = model_fit.____['Intercept']
a1 = model_fit.____['times']
e1 = model_fit.____['times']

# Print the results with more meaningful names
print('Estimate    of the intercept = {:0.2f}'.format(____))
print('Uncertainty of the intercept = {:0.2f}'.format(____))
print('Estimate    of the slope = {:0.2f}'.format(____))
print('Uncertainty of the slope = {:0.2f}'.format(____))

Editar y ejecutar código