Distribuições de entrada incorretas

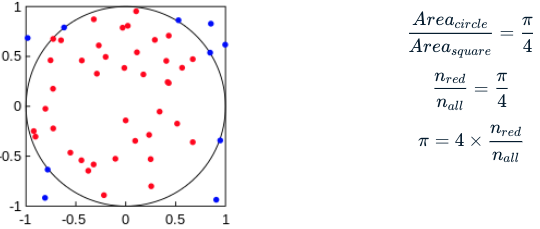
Você continuará trabalhando com o exemplo de pi neste exercício: A graph of a circle inside a square with randomly sampled points

O que acontece se você trocar a distribuição de probabilidade de entrada da distribuição uniforme contínua (random.uniform()) para a distribuição uniforme discreta (random.randint())? Seus resultados não serão confiáveis, porque random.randint() amostra números inteiros discretos, enquanto random.uniform() amostra números de ponto flutuante contínuos.

Preste atenção ao valor de pi estimado que esta simulação gera. Como a distribuição de probabilidade incorreta foi selecionada, ele não será muito preciso! Escolher as distribuições de probabilidade corretas é essencial para simulações de Monte Carlo, e vamos detalhar mais sobre diferentes distribuições nas próximas lições para que você se sinta confiante ao escolher a adequada daqui para frente.

random já foi importado para você.

Este exercício faz parte do curso

Simulações de Monte Carlo em Python

Ver curso

Instruções do exercício

Ame amostrar as coordenadas x e y no intervalo de -1 a 1 usando random.randint() em vez da função correta random.uniform() utilizada no vídeo.

Exercício interativo prático

Experimente este exercício completando este código de exemplo.

n = 10000
circle_points = 0 
square_points = 0 
for i in range(n):
    # Sample the x and y coordinates from -1 to 1 using random.randint()
    x = ____
    y = ____
    dist_from_origin = x**2 + y**2
    if dist_from_origin <= 1:
        circle_points += 1
    square_points += 1
pi = 4 * circle_points / square_points
print(pi)

Editar e executar o código