Calculando o número esperado de contagens

Nos exercícios anteriores, você calculou a média e a variância dos dados de caranguejos e determinou que elas não são iguais. Neste exercício, você vai praticar outra análise de sobredispersão usando a média já calculada para determinar o número esperado de contagens para um certo valor de contagem, por exemplo, contagens iguais a zero. Em outras palavras, qual número de caranguejos com zero satélites devemos esperar na amostra, dada a média amostral calculada.

Lembre-se da figura do conjunto de dados crab, onde é possível notar um grande número de contagens zero.

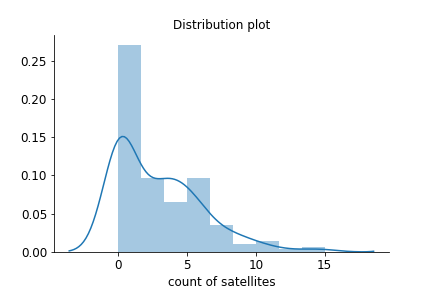
Lembre-se de que, para calcular o número esperado de contagens dado o parâmetro, você pode usar a distribuição de Poisson, definida por

$$ P(y)=\frac{\lambda^ye^{-\lambda}}{y!} $$

O conjunto de dados crab e a média calculada sat_mean já estão carregados no ambiente de trabalho.

Este exercício faz parte do curso

Modelos Lineares Generalizados em Python

Ver curso

Instruções do exercício

Usando a média calculada sat_mean e contagens zero $y = 0$, calcule o número esperado de contagens zero. Use factorial() do math.
Calcule o número de observações com contagens zero na variável sat usando sum() e o número total de observações na amostra usando len().
Imprima a razão entre o número real de observações com contagem zero e o número total de observações.

Exercício interativo prático

Experimente este exercício completando este código de exemplo.

# Expected number of zero counts
exp_zero_cnt = ((____**____)*np.____(-____))/math.____(____)

# Print exp_zero_counts
print('Expected zero counts given mean of ', round(____,3), 
      'is ', round(____,3)*100)

# Number of zero counts in sat variable
actual_zero_cnt = sum(____[____]  == 0)

# Number of observations in crab dataset
num_obs = len(____)

# Print the percentage of zero count observations in the sample
print('Actual zero counts in the sample: ', round(____ / ____,3)*100)

Editar e executar o código