Taxa de variação na probabilidade

Para o conjunto de dados wells, você já ajustou um modelo de regressão logística com a fórmula switch ~ distance100, obtendo o seguinte ajuste $$ log(\frac{\mu}{1-\mu}) = 0.6060 - 0.6219\times distance100 $$

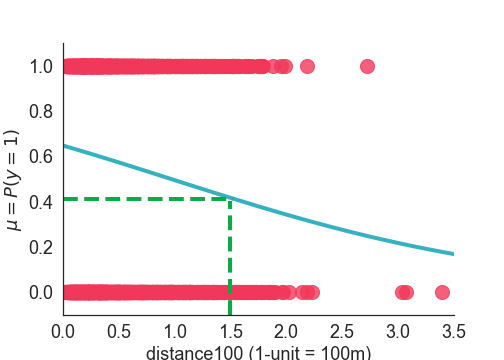
Neste exercício, você vai usar esse modelo para entender como a probabilidade estimada muda em um certo valor de distance100, digamos 1.5, como mostrado na figura abaixo.

Lembre-se das fórmulas para o logito inverso (probabilidade)

$$ \mu = \frac{exp(\beta_0+\beta_1x_1)}{1+exp(\beta_0+\beta_1x_1)} $$

e da inclinação da reta tangente do ajuste do modelo no ponto \(x\):

$$ \beta*\mu(1-\mu) $$

O conjunto de dados wells e o modelo wells_GLM estão carregados no espaço de trabalho.