Logistische Regressionsalgorithmus
Schauen wir uns die Interna an und implementieren einen Algorithmus für logistische Regression. Da Rs glm()-Funktion sehr komplex ist, beschränkst du dich darauf, eine einfache logistische Regression für einen einzelnen Datensatz zu implementieren.
Anstelle der Summe der Quadrate als Metrik möchten wir die Likelihood verwenden. Die Log-Likelihood ist numerisch stabiler, daher verwenden wir diese. Es gibt noch eine Änderung: Wir wollen die Log-Likelihood maximieren, aber optim() sucht standardmäßig nach Minimalwerten. Daher ist es einfacher, die negative Log-Likelihood zu berechnen.
Der Log-Likelihood-Wert für jede Beobachtung ist
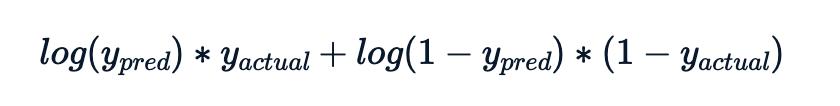
Die zu berechnende Metrik ist das Minus der Summe dieser Log-Likelihood-Beiträge.
Die erklärenden Werte (die Spalte time_since_last_purchase von churn) stehen als x_actual zur Verfügung.
Die Antwortwerte (die Spalte has_churned von churn) stehen als y_actual zur Verfügung.
Diese Übung ist Teil des Kurses
Fortgeschrittene Regression in R
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# Set the intercept to 1
intercept <- ___
# Set the slope to 0.5
slope <- ___
# Calculate the predicted y values
y_pred <- ___
# Calculate the log-likelihood for each term
log_likelihoods <- ___
# Calculate minus the sum of the log-likelihoods for each term
___