ComeçarComece de graça

Input transforms: the "hockey stick"

In this exercise, we will build a model to predict price from a measure of the house's size (surface area). The houseprice dataset, loaded for you, has the columns:

  • price: house price in units of $1000
  • size: surface area

A scatterplot of the data shows that the data is quite non-linear: a sort of "hockey-stick" where price is fairly flat for smaller houses, but rises steeply as the house gets larger. Quadratics and tritics are often good functional forms to express hockey-stick like relationships. Note that there may not be a "physical" reason that price is related to the square of the size; a quadratic is simply a closed form approximation of the observed relationship.

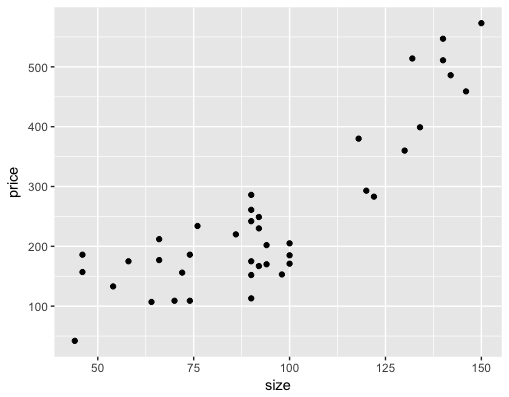
scatterplot

You will fit a model to predict price as a function of the squared size, and look at its fit on the training data.

Because ^ is also a symbol to express interactions, use the function I() (docs) to treat the expression x^2 “as is”: that is, as the square of x rather than the interaction of x with itself.

exampleFormula = y ~ I(x^2)

Este exercício faz parte do curso

Supervised Learning in R: Regression

Ver curso

Instruções do exercício

  • Write a formula, fmla_sqr, to express price as a function of squared size. Print it.
  • Fit a model model_sqr to the data using fmla_sqr
  • For comparison, fit a linear model model_lin to the data using the formula price ~ size.
  • Fill in the blanks to
    • make predictions from the training data from the two models
    • pivot the predictions into a single column pred using pivot_longer().
    • graphically compare the predictions of the two models to the data. Which fits better?

Exercício interativo prático

Experimente este exercício completando este código de exemplo.

# houseprice is available
summary(houseprice)

# Create the formula for price as a function of squared size
(fmla_sqr <- ___)

# Fit a model of price as a function of squared size (use fmla_sqr)
model_sqr <- ___

# Fit a model of price as a linear function of size
model_lin <- ___

# Make predictions and compare
houseprice %>% 
    mutate(pred_lin = ___(___),       # predictions from linear model
           pred_sqr = ___(___)) %>%   # predictions from quadratic model
    pivot_longer(cols = c('pred_lin', 'pred_sqr'), names_to = 'modeltype', values_to = 'pred') %>% # pivot the predictions
    ggplot(aes(x = size)) + 
       geom_point(aes(y = ___)) +                   # actual prices
       geom_line(aes(y = ___, color = modeltype)) + # the predictions
       scale_color_brewer(palette = "Dark2")
Editar e executar o código