Algorithme de régression logistique
Plongeons dans les entrailles du modèle et implémentons un algorithme de régression logistique. Comme la fonction glm() de R est très complexe, vous allez vous limiter à implémenter une régression logistique simple pour un jeu de données unique.
Plutôt que d’utiliser la somme des carrés comme métrique, nous allons utiliser la vraisemblance. Cependant, la log-vraisemblance est plus stable numériquement ; nous utiliserons donc celle-ci. En fait, il y a un dernier changement : comme nous voulons maximiser la log-vraisemblance, mais que optim() cherche par défaut des minima, il est plus simple de calculer la log-vraisemblance négative.
La valeur de log-vraisemblance pour chaque observation est
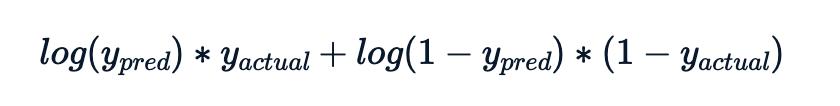
La métrique à calculer est l’opposé de la somme de ces contributions de log-vraisemblance.
Les valeurs explicatives (la colonne time_since_last_purchase de churn) sont disponibles sous le nom x_actual.
Les valeurs de réponse (la colonne has_churned de churn) sont disponibles sous le nom y_actual.
Cet exercice fait partie du cours
Régression intermédiaire en R
Exercice interactif pratique
Essayez cet exercice en complétant cet exemple de code.
# Set the intercept to 1
intercept <- ___
# Set the slope to 0.5
slope <- ___
# Calculate the predicted y values
y_pred <- ___
# Calculate the log-likelihood for each term
log_likelihoods <- ___
# Calculate minus the sum of the log-likelihoods for each term
___