Algoritmo de regresión logística
Vamos a profundizar en el funcionamiento interno e implementar un algoritmo de regresión logística. Como la función glm() de R es muy compleja, nos limitaremos a implementar una regresión logística simple para un único conjunto de datos.
En lugar de usar la suma de cuadrados como métrica, queremos usar la verosimilitud. Sin embargo, la log-verosimilitud es más estable computacionalmente, así que usaremos esa. De hecho, hay un cambio más: como queremos maximizar la log-verosimilitud, pero optim() por defecto busca mínimos, es más sencillo calcular la log-verosimilitud negativa.
El valor de la log-verosimilitud para cada observación es
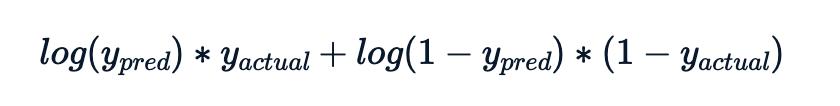
La métrica a calcular es menos la suma de estas contribuciones de log-verosimilitud.
Los valores explicativos (la columna time_since_last_purchase de churn) están disponibles como x_actual.
Los valores de respuesta (la columna has_churned de churn) están disponibles como y_actual.
Este ejercicio forma parte del curso
Regresión intermedia en R
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Set the intercept to 1
intercept <- ___
# Set the slope to 0.5
slope <- ___
# Calculate the predicted y values
y_pred <- ___
# Calculate the log-likelihood for each term
log_likelihoods <- ___
# Calculate minus the sum of the log-likelihoods for each term
___