Rate of change in probability
For the wells dataset you have already fitted a logistic regression model with the model formula switch ~ distance100 obtaining the following fit
$$
log(\frac{\mu}{1-\mu}) = 0.6060 - 0.6219\times distance100
$$
In this exercise you will use that model to understand how the estimated probability changes at a certain value of distance100, say 1.5 as depicted in the figure below.
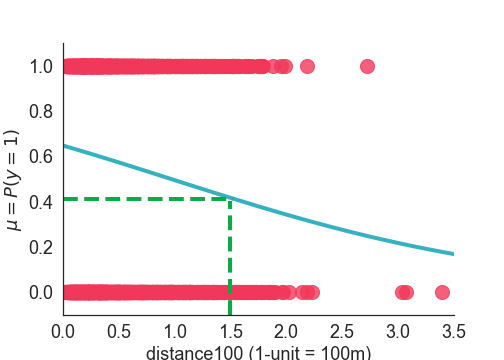
Recall the formulas for the inverse-logit (probability)
$$ \mu = \frac{exp(\beta_0+\beta_1x_1)}{1+exp(\beta_0+\beta_1x_1)} $$
and the slope of the tangent line of the model fit at point \(x\):
$$ \beta*\mu(1-\mu) $$
Dataset wells and the model wells_GLM are loaded in the workspace.
Deze oefening maakt deel uit van de cursus
Generalized Linear Models in Python
Praktische interactieve oefening
Probeer deze oefening eens door deze voorbeeldcode in te vullen.
# Define x at 1.5
x = ____
# Extract intercept & slope from the fitted model
intercept, slope = ____.____