Distribuciones de entrada erróneas

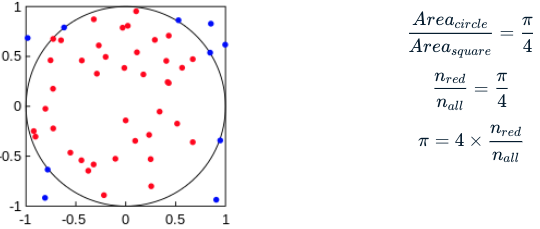
En este ejercicio, seguirás trabajando con el ejemplo de pi: Gráfico de un círculo dentro de un cuadrado con puntos muestreados aleatoriamente

¿Qué ocurre si cambias la distribución de probabilidad de entrada de la distribución uniforme continua(random.uniform()) a la distribución uniforme discreta(random.randint())? Tus resultados no serán fiables, porque random.randint() muestrea números enteros discretos, mientras que random.uniform() muestrea números flotantes continuos.

Presta atención al valor estimado de pi que genera esta simulación. Como se ha seleccionado una distribución de probabilidad incorrecta, ¡no será muy exacta! Elegir las distribuciones de probabilidad correctas es esencial para las simulaciones de Montecarlo, y entraremos en más detalles sobre las distintas distribuciones en lecciones posteriores para que te sientas seguro de elegir la correcta en adelante.

random se ha importado para ti.

Este ejercicio forma parte del curso

Simulaciones Montecarlo en Python

Ver curso

Instrucciones de ejercicio

Muestrea las coordenadas x y y en el intervalo de -1 a 1 utilizando random.randint() en lugar de la función correcta random.uniform() utilizada en el vídeo.

Ejercicio interactivo práctico

Pruebe este ejercicio completando este código de muestra.

n = 10000
circle_points = 0 
square_points = 0 
for i in range(n):
    # Sample the x and y coordinates from -1 to 1 using random.randint()
    x = ____
    y = ____
    dist_from_origin = x**2 + y**2
    if dist_from_origin <= 1:
        circle_points += 1
    square_points += 1
pi = 4 * circle_points / square_points
print(pi)

Editar y ejecutar código