Calcular el número esperado de conteos

En los ejercicios anteriores calculaste la media y la varianza de los datos de cangrejos y comprobaste que no son iguales. En este ejercicio practicarás otro análisis de sobredispersión usando la media ya calculada para obtener el número esperado de conteos para un cierto valor, por ejemplo, los conteos cero. Dicho de otro modo, ¿cuántos satélites cero deberíamos esperar en la muestra dada la media muestral calculada?

Recuerda la figura del conjunto de datos crab, donde se aprecia un gran número de conteos cero.

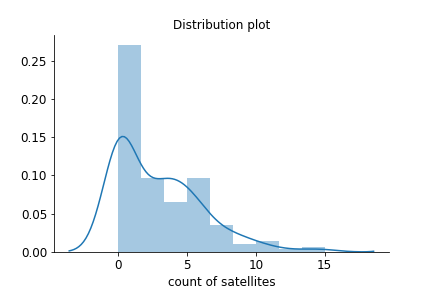
Recuerda que para calcular el número esperado de conteos dado el parámetro puedes usar la distribución de Poisson, definida por

$$ P(y)=\frac{\lambda^y e^{-\lambda}}{y!} $$

El conjunto de datos crab y la media calculada sat_mean están precargados en el espacio de trabajo.

Este ejercicio forma parte del curso

Modelos lineales generalizados en Python

Ver curso

Instrucciones del ejercicio

Usando la media calculada sat_mean y los conteos cero $y = 0$, calcula el número esperado de conteos cero. Usa math factorial().
Calcula el número de observaciones con conteos cero en la variable sat usando sum() y el número total de observaciones de la muestra usando len().
Imprime la razón entre las observaciones reales con conteo cero y el número total de observaciones.

Ejercicio interactivo práctico

Prueba este ejercicio y completa el código de muestra.

# Expected number of zero counts
exp_zero_cnt = ((____**____)*np.____(-____))/math.____(____)

# Print exp_zero_counts
print('Expected zero counts given mean of ', round(____,3), 
      'is ', round(____,3)*100)

# Number of zero counts in sat variable
actual_zero_cnt = sum(____[____]  == 0)

# Number of observations in crab dataset
num_obs = len(____)

# Print the percentage of zero count observations in the sample
print('Actual zero counts in the sample: ', round(____ / ____,3)*100)

Editar y ejecutar código