Tasa de cambio en la probabilidad
Para el conjunto de datos wells ya has ajustado un modelo de regresión logística con la fórmula switch ~ distance100, obteniendo el siguiente ajuste
$$
log(\frac{\mu}{1-\mu}) = 0.6060 - 0.6219\times distance100
$$
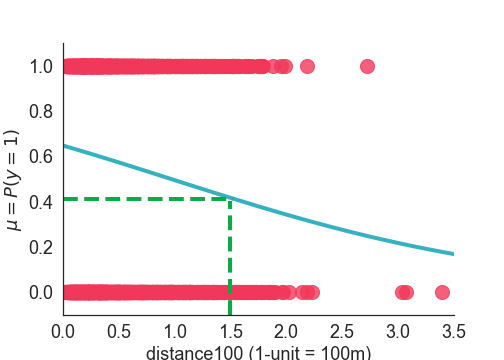
En este ejercicio usarás ese modelo para entender cómo cambia la probabilidad estimada en un cierto valor de distance100, por ejemplo 1.5, como se muestra en la figura de abajo.
Recuerda las fórmulas para la inversa del logit (probabilidad)
$$ \mu = \frac{exp(\beta_0+\beta_1x_1)}{1+exp(\beta_0+\beta_1x_1)} $$
y la pendiente de la recta tangente del ajuste del modelo en el punto \(x\):
$$ \beta*\mu(1-\mu) $$
El conjunto de datos wells y el modelo wells_GLM están cargados en el espacio de trabajo.
Este ejercicio forma parte del curso
Modelos lineales generalizados en Python
Ejercicio interactivo práctico
Prueba este ejercicio y completa el código de muestra.
# Define x at 1.5
x = ____
# Extract intercept & slope from the fitted model
intercept, slope = ____.____