Binomialverteilung
In der vorherigen Übung hast du die Bernoulli-Versuche modelliert. Die Binomialverteilung ist die Summe der Anzahl erfolgreicher Ergebnisse in einer Reihe von Bernoulli-Versuchen.
Die Notation der Binomialverteilung ist \(B(n, p)\), wobei \(n\) die Anzahl der Experimente und \(p\) die Erfolgswahrscheinlichkeit ist.
Für diese Übung betrachten wir 10 aufeinanderfolgende faire Münzwürfe. Du wettest auf Zahl und betrachtest dieses Ergebnis eines Münzwurfs als Erfolg.
Zur Erinnerung:
dbinom(x = k, size = n, prob = p)berechnet \(P(X = k)\) für \(X \sim B(n, p)\),pbinom(q = k, size = n, prob = p)berechnet \(P(X \le k)\) für \(X \sim B(n, p)\).
Denk daran, dass für diskrete Verteilungen, die ganze Zahlen annehmen, gilt: \(P(X \ge k) = 1 - P(X \le k-1)\).
Zum Beispiel:
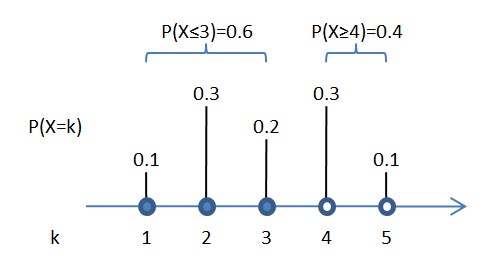
Also gilt: \(P(X \ge 4) = 1 - P(X \le 3)\).
Diese Übung ist Teil des Kurses
Statistik-Interviewfragen in R üben
Anleitung zur Übung
- Weise die Wahrscheinlichkeit, genau 6-mal Zahl zu erhalten,
six_tailszu und gib das Ergebnis aus. - Weise die Wahrscheinlichkeit, 7-mal oder weniger Zahl zu erhalten,
seven_or_lesszu und gib das Ergebnis aus. - Weise die Wahrscheinlichkeit, 5-mal oder mehr Zahl zu erhalten,
five_or_morezu und gib das Ergebnis aus.
Interaktive Übung
Vervollständige den Beispielcode, um diese Übung erfolgreich abzuschließen.
# The probability of getting 6 tails
six_tails <- ___(___ = ___, size = ___, prob = ___)
print(six_tails)
# The probability of getting 7 or less tails
seven_or_less <- ___(___ = ___, size = ___, prob = ___)
print(seven_or_less)
# The probability of getting 5 or more tails
five_or_more <- 1 - ___(___ = ___, size = ___, prob = ___)
print(five_or_more)