Calculer le nombre attendu de comptages

Dans les exercices précédents, vous avez calculé la moyenne et la variance des données sur les crabes et constaté qu’elles ne sont pas égales. Dans cet exercice, vous allez pratiquer une autre analyse de la surdispersion en utilisant la moyenne déjà calculée et en déterminant le nombre attendu de comptages pour une valeur donnée, par exemple les zéros. En d’autres termes, combien de zéros de satellites doit-on s’attendre à observer dans l’échantillon, étant donné la moyenne observée.

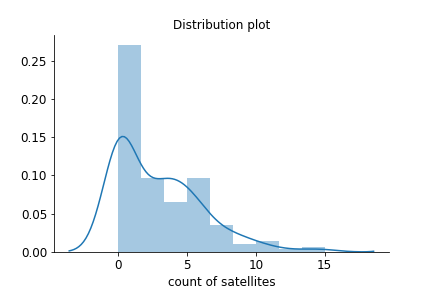
Repensez au graphique du jeu de données crab, où l’on remarque un grand nombre de zéros.

Rappelez-vous que pour calculer le nombre attendu de comptages étant donné le paramètre, vous pouvez utiliser la loi de Poisson définie par

$$ P(y)=\frac{\lambda^ye^{-\lambda}}{y!} $$

Le jeu de données crab et la moyenne calculée sat_mean sont déjà chargés dans l’espace de travail.

Cet exercice fait partie du cours

Modèles linéaires généralisés en Python

Afficher le cours

Instructions

En utilisant la moyenne sat_mean et les zéros $y = 0$, calculez le nombre attendu de zéros. Utilisez math factorial().
Calculez le nombre d’observations avec un comptage nul dans la variable sat à l’aide de sum() et le nombre total d’observations dans l’échantillon à l’aide de len().
Affichez le ratio entre le nombre réel d’observations nulles et le nombre total d’observations.

Exercice interactif pratique

Essayez cet exercice en complétant cet exemple de code.

# Expected number of zero counts
exp_zero_cnt = ((____**____)*np.____(-____))/math.____(____)

# Print exp_zero_counts
print('Expected zero counts given mean of ', round(____,3), 
      'is ', round(____,3)*100)

# Number of zero counts in sat variable
actual_zero_cnt = sum(____[____]  == 0)

# Number of observations in crab dataset
num_obs = len(____)

# Print the percentage of zero count observations in the sample
print('Actual zero counts in the sample: ', round(____ / ____,3)*100)

Modifier et exécuter le code