Rate of change in probability

For the wells dataset you have already fitted a logistic regression model with the model formula switch ~ distance100 obtaining the following fit $$ log(\frac{\mu}{1-\mu}) = 0.6060 - 0.6219\times distance100 $$

In this exercise you will use that model to understand how the estimated probability changes at a certain value of distance100, say 1.5 as depicted in the figure below.

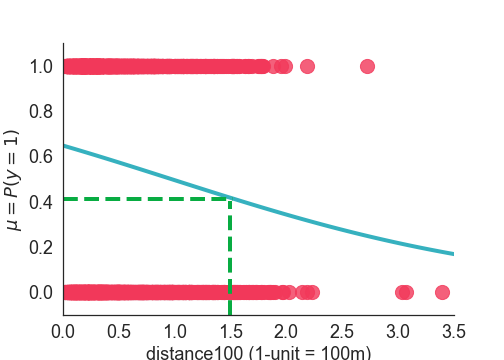
Recall the formulas for the inverse-logit (probability)

$$ \mu = \frac{exp(\beta_0+\beta_1x_1)}{1+exp(\beta_0+\beta_1x_1)} $$

and the slope of the tangent line of the model fit at point \(x\):

$$ \beta*\mu(1-\mu) $$

Dataset wells and the model wells_GLM are loaded in the workspace.