Distribución uniforme

En entrevistas suelen aparecer preguntas sobre la distribución uniforme continua porque los cálculos asociados son relativamente sencillos.

Una variable aleatoria suele denotarse como \(X\) y una distribución uniforme continua en el intervalo \([a, b]\) se denota \(U(a, b)\).

Recuerda que punif(q = k, min = a, max = b) calcula \(P(X \le k)\) para \(X \sim U(a, b)\).

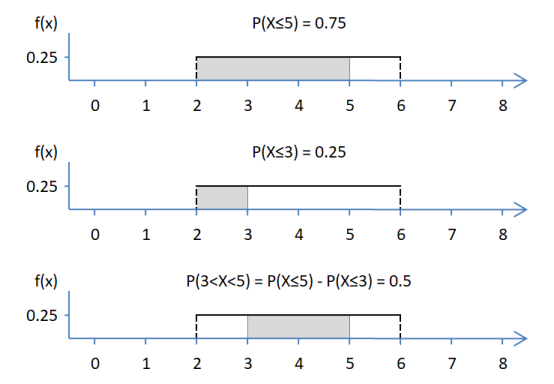
Puedes obtener la probabilidad de que una variable aleatoria caiga en un intervalo como la diferencia entre dos probabilidades acumuladas: \(P(j < X < k) = P(X \le k) - P(X \le j)\)

Mira el ejemplo siguiente para \(X \sim U(2, 6)\):